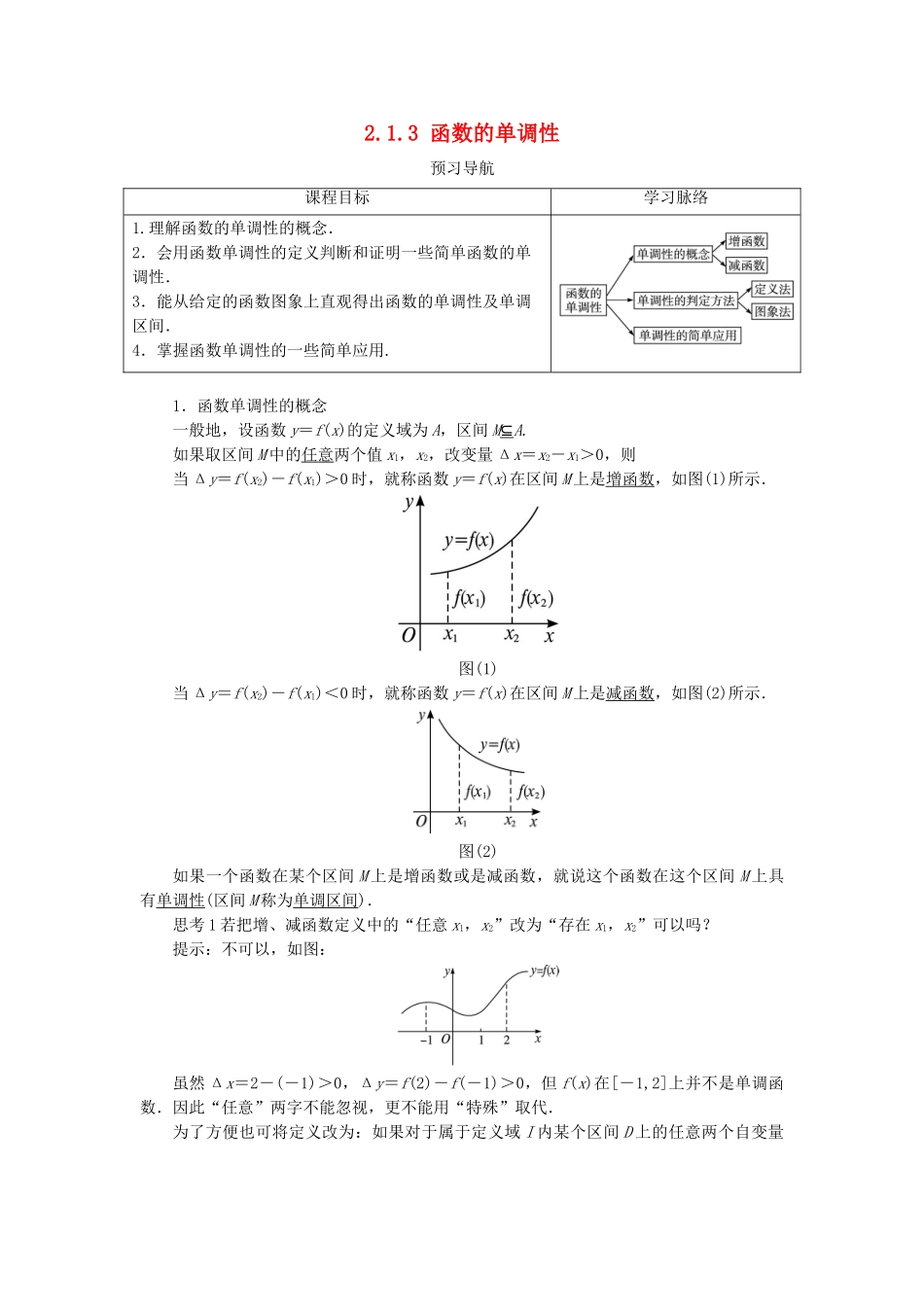
2.1.3 函数的单调性预习导航课程目标学习脉络1.理解函数的单调性的概念.2.会用函数单调性的定义判断和证明一些简单函数的单调性.3.能从给定的函数图象上直观得出函数的单调性及单调区间.4.掌握函数单调性的一些简单应用.1.函数单调性的概念一般地,设函数 y=f(x)的定义域为 A,区间 M⊆A.如果取区间 M 中的任意两个值 x1,x2,改变量 Δx=x2-x1>0,则当 Δy=f(x2)-f(x1)>0 时,就称函数 y=f(x)在区间 M 上是增函数,如图(1)所示.图(1)当 Δy=f(x2)-f(x1)<0 时,就称函数 y=f(x)在区间 M 上是减函数,如图(2)所示.图(2)如果一个函数在某个区间 M 上是增函数或是减函数,就说这个函数在这个区间 M 上具有单调性(区间 M 称为单调区间).思考 1 若把增、减函数定义中的“任意 x1,x2”改为“存在 x1,x2”可以吗?提示:不可以,如图:虽然 Δx=2-(-1)>0,Δy=f(2)-f(-1)>0,但 f(x)在[-1,2]上并不是单调函数.因此“任意”两字不能忽视,更不能用“特殊”取代.为了方便也可将定义改为:如果对于属于定义域 I 内某个区间 D 上的任意两个自变量的值 x1,x2,当 x1≠x2时,总有>0(<0),那么就说函数 f(x)在区间 D 上是增(减)函数.思考 2“函数 y=在区间(-∞,0)∪(0,+∞)上是减函数”是否正确?提示:不正确,函数 y=的单调区间不能取并集,应写为(-∞,0),(0,+∞)或(-∞,0)和(0,+∞).思考 3“函数 f(x)的单调增(减)区间是 D”与“函数 f(x)在区间 D 上是增(减)函数”是否相同?提示:不相同.函数 f(x)的单调增(减)区间是 D,这一说法意味着除 D 之外,函数f(x)再无其他单调增(减)区间.函数 f(x)在区间 D 上是增(减)函数,则意味着区间 D 是函数 f(x)的单调增(减)区间的子区间,即除区间 D 外,函数 f(x)还可能有其他的单调增(减)区间.2.判断函数单调性的步骤利用定义证明函数 f(x)在给定的区间 M 上的单调性的一般步骤:(1)任取 x1,x2∈M,且 Δx=x2-x1>0;(2)作差:Δy=f ( x 2) - f ( x 1);(3)变形(通常所用的方法有:因式分解、配方、分子有理化、分母有理化、通分等);(4)定号(即判断 Δ y 的正负);(5)下结论(即指出函数 f(x)在给定的区间 M 上的单调性).