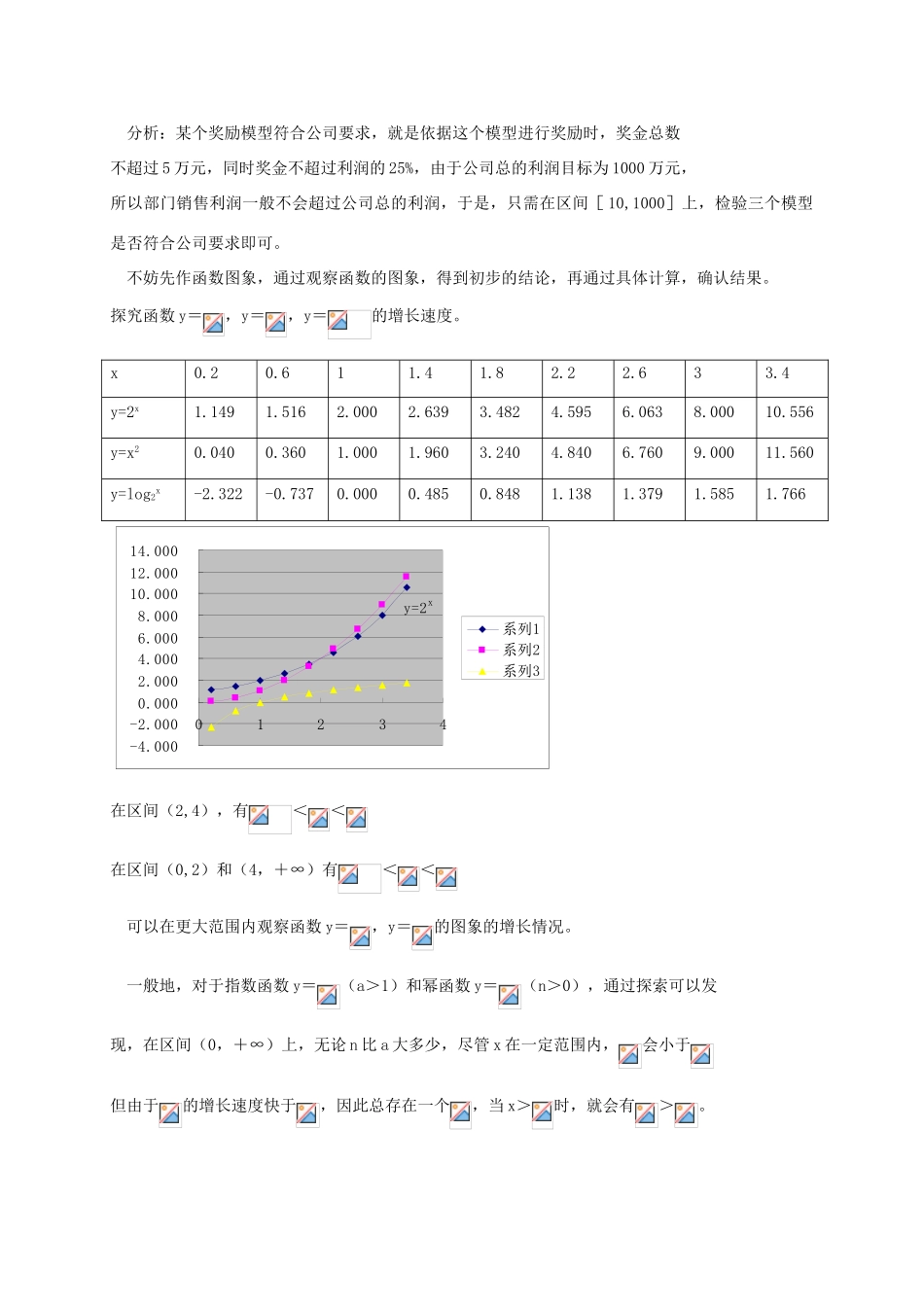
3.2.1 几类不同增长的函数模型学习过程一、复习提问 写出指数函数、对数函数、幂函数的一般形式,你知道它们的变化规律吗?二、新课 例 1、假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下: 方案一:每天回报 40 元; 方案二:第一天回报 10 元,以后每天比前一天多回报 10 元; 方案三:第一天回报 0.4 元,以后每天的回报比前一天翻一番。 请问,你会选择哪种投资方案? 解:设第 x 天所得回报是 y 元,则各方案的函数模型为:方案一:y=40(x∈N+)方案二:y=10x(x∈N+)方案三:y=0.4×(x∈N+)方案一是常数函数,方案二是增函数,呈直线型增长,方案三也是增函数,呈指数型增长,增长速度比其它 2 个方案快得多,称为“指数爆炸”。 投资 5 天以下选方案一,投资 5――8 天选方案二,投资 8 天以上选方案三。 再看累计回报数表 P114。投资 8 天以下(不含 8 天),应选择第一种投资方案,投资 8--10 天,应选择第二种投资方案;投资 11 天(含 11 天)以上,则应选择第三种方案。 例 2、某公司为了实现 1000 万元利润目标,准备制定一个激励销售部门的奖励方案:在销售利润达到 10 万元时,按销售利润进行奖励,且奖金 y(单位:万元)随销售利润 x(单位:万元)的增加而增加,但奖金总数不超过 5 万元,同时奖金不超过利润的 25%。现有三个奖励模型:y=0.25x,y=+1,y=1.002x。其中哪个模型能符合公司的要求?········xy024 6 8 10 1214012010080604020· · · · · ···· · · · · ···y=40········y=10xy=0.4×2x-1 分析:某个奖励模型符合公司要求,就是依据这个模型进行奖励时,奖金总数不超过 5 万元,同时奖金不超过利润的 25%,由于公司总的利润目标为 1000 万元,所以部门销售利润一般不会超过公司总的利润,于是,只需在区间[ 10,1000]上,检验三个模型是否符合公司要求即可。 不妨先作函数图象,通过观察函数的图象,得到初步的结论,再通过具体计算,确认结果。探究函数 y=,y=,y=的增长速度。x0.20.611.41.82.22.633.4y=2x1.149 1.516 2.000 2.639 3.482 4.595 6.063 8.000 10.556 y=x20.040 0.360 1.000 1.960 3.240 4.840 6.760 9.000 11.560 y=log2x-2.322 -0.737 0.000 0.485 0.848 1.138 1.379 1.585 1.766 -4.000-2.0000.0002.0004...