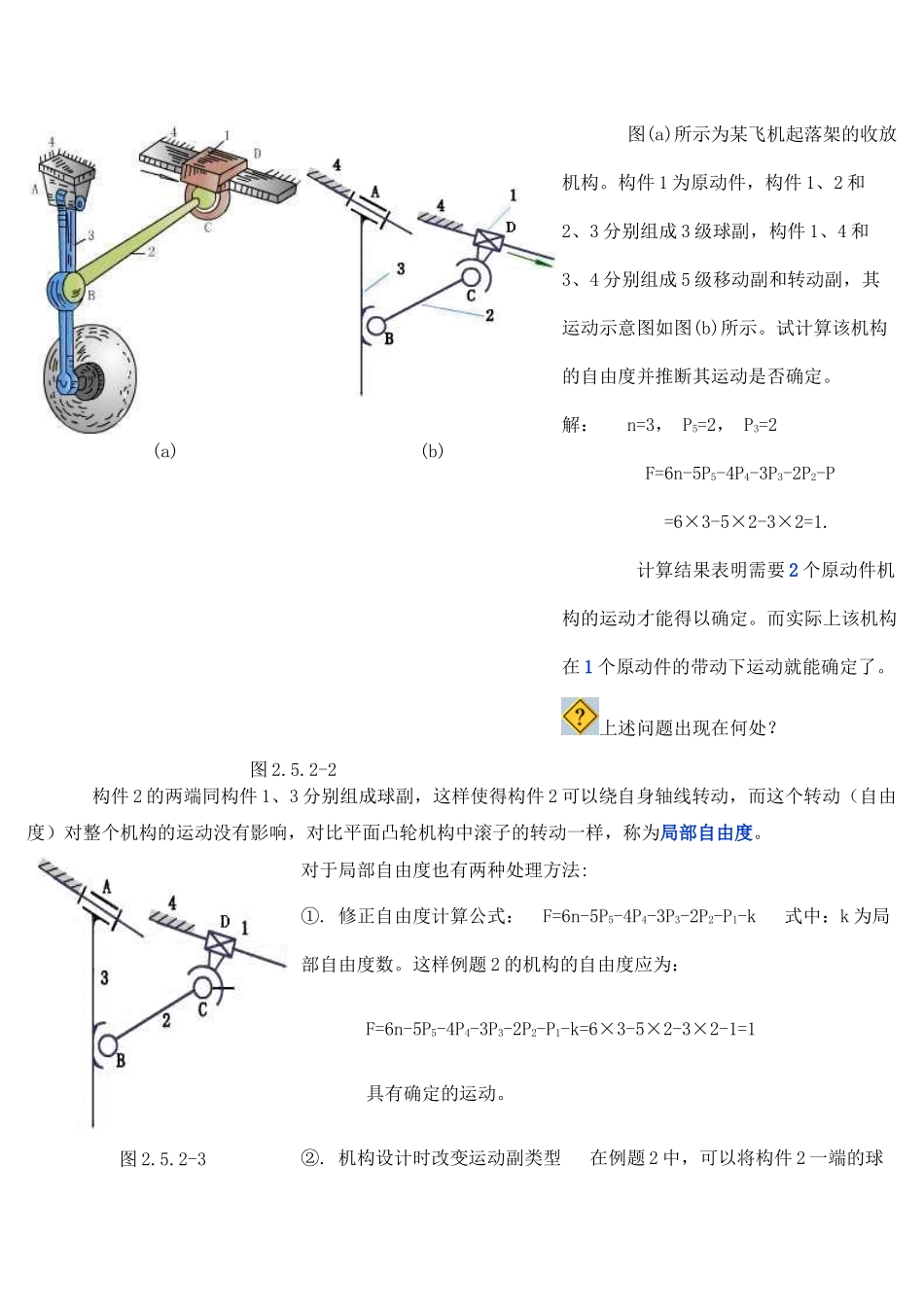
2.5.2 空间机构的自由度计算 同平面机构自由度计算公式推导过程一样,空间机构的自由度 = 所有活动构件自由度 - 所有运动副引入的约束数,其公式为:F=6n-5P5-4P4-3P3-2P2-P1式中:n 为活动构件数; P1、P2、P3、P4、P5分别为 1 ~ 5 级运动副的个数。例 题 一(a) (b) 图 2.5.2-1 图(a)所示为自动驾驶仪操纵装置内的空间四杆机构。活塞 2 相对气缸运动后通过连杆 3 使摇杆 4 作定轴转动。构件 1、2 组成圆柱副,构件 2、3 和构件 4、1 分别组成转动副,构件 3、4 组成球面副,其运动示意图如图(b)所示。试计算该机构的自由度。解: n=3, P5=2, P4=1, P3=1 F=6n-5P5-4P4-3P3-2P2-P =6×3-5×2-4×1-3×1=1. 例 题 二 图(a)所示为某飞机起落架的收放机构。构件 1 为原动件,构件 1、2 和2、3 分别组成 3 级球副,构件 1、4 和3、4 分别组成 5 级移动副和转动副,其运动示意图如图(b)所示。试计算该机构的自由度并推断其运动是否确定。解: n=3, P5=2, P3=2 F=6n-5P5-4P4-3P3-2P2-P =6×3-5×2-3×2=1. 计算结果表明需要 2 个原动件机构的运动才能得以确定。而实际上该机构在 1 个原动件的带动下运动就能确定了。上述问题出现在何处?(a) (b) 图 2.5.2-2 构件 2 的两端同构件 1、3 分别组成球副,这样使得构件 2 可以绕自身轴线转动,而这个转动(自由度)对整个机构的运动没有影响,对比平面凸轮机构中滚子的转动一样,称为局部自由度。图 2.5.2-3 对于局部自由度也有两种处理方法:①. 修正自由度计算公式: F=6n-5P5-4P4-3P3-2P2-P1-k 式中:k 为局部自由度数。这样例题 2 的机构的自由度应为: F=6n-5P5-4P4-3P3-2P2-P1-k=6×3-5×2-3×2-1=1 具有确定的运动。②. 机构设计时改变运动副类型 在例题 2 中,可以将构件 2 一端的球副设计变成球销副,如图 2.5.2-3 所示,这样就消除了构件 2 绕自身轴线转动的局部自由度。这时机构的自由度应为: F=6n-5P5-4P4-3P3-2P2-P1=6×3-5×2-4×1-3×1=1 具有确定的运动。 由此可以看出,空间机构中同样可能存在有局部自由度、虚约束等问题,在计算机构自由度时应加以注意推断,进行正确的处理。