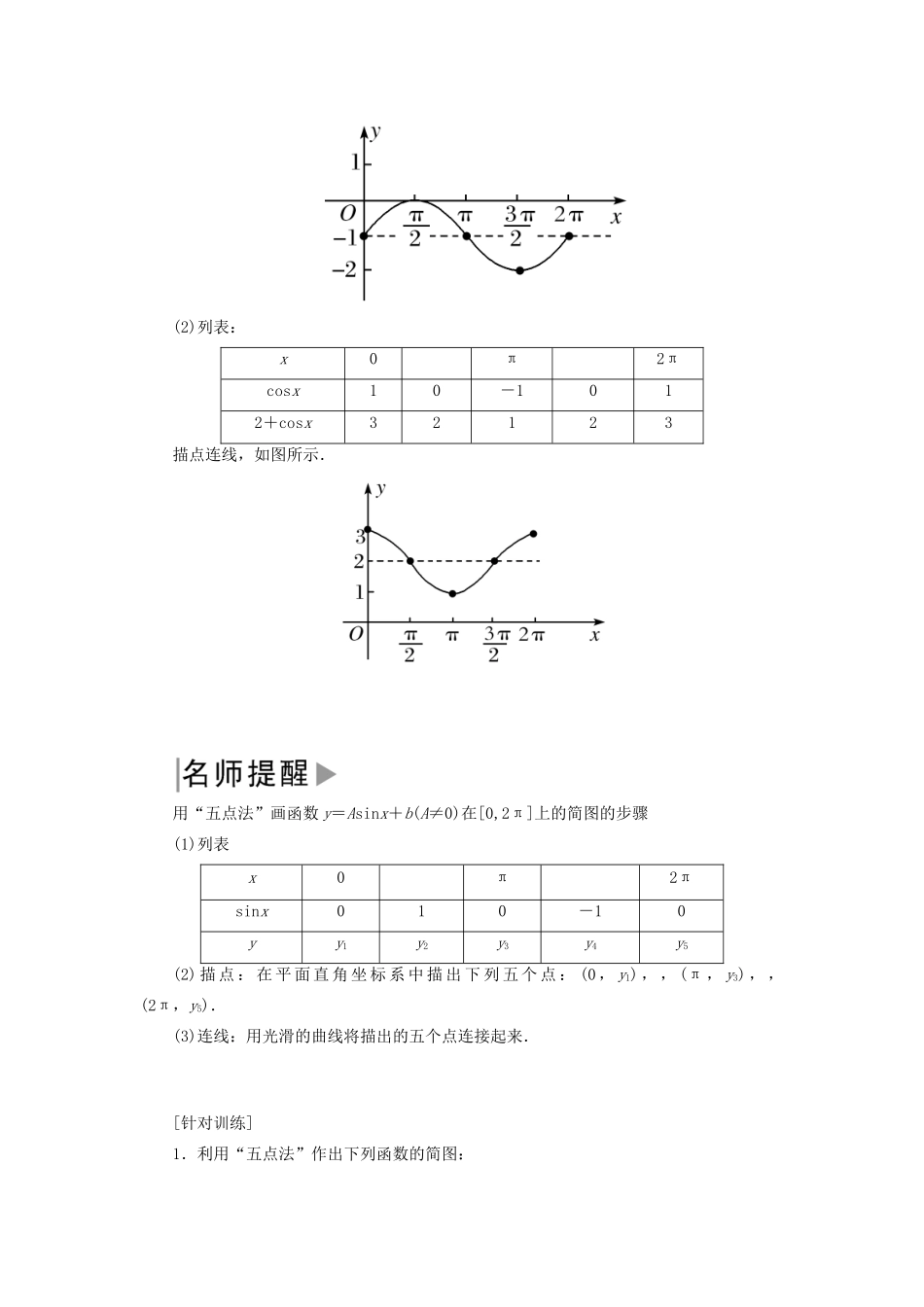
5.4.1 正弦函数、余弦函数的图象1.了解正弦函数、余弦函数的图象.2.会用“五点法”画出正弦函数、余弦函数的图象.3.能利用正弦函数、余弦函数的图象解决简单问题.1.正弦曲线正弦函数 y=sinx,x∈R 的图象叫正弦曲线,是一条“波浪起伏”的连续光滑曲线.2.正弦函数图象的画法(1)几何法① 利用正弦线画出 y=sinx,x∈[0,2π]的图象;② 将图象向左、向右平行移动(每次 2π 个单位长度).(2)五点法① 画出正弦曲线在[0,2π]上的图象的五个关键点(0,0),,(π , 0) ,,(2π , 0) ,用光滑的曲线连接;② 将所得图象向左、向右平行移动(每次 2π 个单位长度).3.余弦曲线余弦函数 y=cosx,x∈R 的图象叫余弦曲线.它是与正弦曲线具有相同形状的“波浪起伏”的连续光滑曲线.4.余弦函数图象的画法(1)要得到 y=cosx 的图象,只需把 y=sinx 的图象向左平移个单位长度即可,这是由于 cosx=sin.(2)用“五点法”:画余弦曲线 y=cosx 在[0,2π]上的图象时,所取的五个关键点分别为(0,1),,(π ,- 1) ,,(2π , 1) ,再用光滑的曲线连接.温馨提示:(1)“五点法”作图中的“五点”是指函数的最高点、最低点以及图象与坐标轴的交点,这是作正弦函数、余弦函数图象最常用的方法.(2)“五点法”画正弦函数、余弦函数的图象时要注意图象的对称性和凸凹方向.判断正误(正确的打“√”,错误的打“×”)(1)函数 y=cosx 的图象与 y 轴只有一个交点.( )(2)将正弦曲线向右平移个单位就得到余弦曲线.( )(3)函数 y=sinx,x∈的图象与函数 y=cosx,x∈[0,2π]的图象的形状完全一致.( )(4) 函 数 y = sinx , x∈[2kπ , 2(k + 1)π]k∈Z , 且 k≠0 的 图 象 与 y =sinx,x∈[0,2π]的图象形状完全一致.( )[答案] (1)√ (2)× (3)√ (4)√题型一用“五点法”作简图【典例 1】 用“五点法”作出下列函数的简图.(1)y=sinx-1,x∈[0,2π];(2)y=2+cosx,x∈[0,2π].[思路导引] 利用“五点法”作函数简图时,应先列表,再描点,再连线.[解] (1)列表:x0π2πsinx010-10sinx-1-10-1-2-1描点连线,如图所示.(2)列表:x0π2πcosx10-1012+cosx32123描点连线,如图所示.用“五点法”画函数 y=Asinx+b(A≠0)在[0,2π]上的简图的步骤(1)列表x0π2πsinx010-10yy1y2y3y4y5(2) 描 点 : 在 平 面 直 角 坐 标 系 中 描 出 下 列 ...