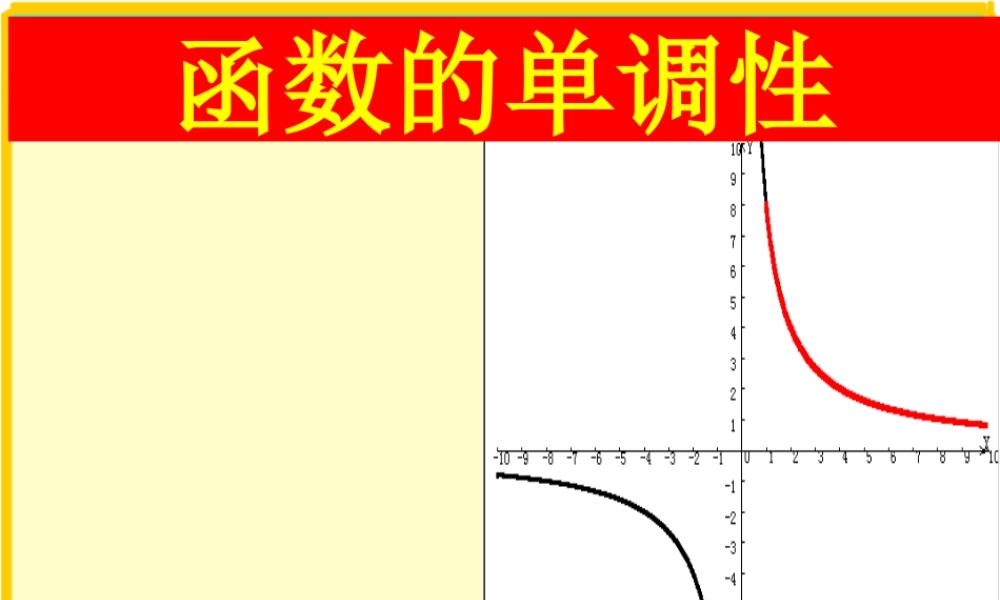
函数的单调性 Oxy1xy11Oxy2x2y21Oxyx2xy2 21yOxx1y 引例:常见函数的图象1 、当 x∈[0 , +∞) , x 增大时, 图( 1 )中的 y 值 ; 图( 2 )中的 y 值 。2 、当 x∈( -∞, 0) , x 增大时, 图( 1 )中的 y 值 ; 图( 2 )中的 y 值 。请观察函数 y=x2 与 y=x3 图象,回答下列问题:增大增大增大减小 ,,21 xx在给定区间上任取21xx )f(x)f(x21 函数 f (x) 在给定区间上为增函数。Oxy)x(fy 如何用 x 与 f(x) 来描述上升的图象?)x(f11x如何用 x 与 f(x) 来描述下降的图象?,,21 xx在给定区间上任取21xx 函数 f (x) 在给定区间上为减函数。)f(x)f(x21 )x(f1)x(f2)x(fy Oxy1x2x)x(f22x一、概念 增函数与减函数 的概念:1. 如果对于属于这个区间的自变量的任意),f(x)都有f(x时,x当x,x,两个值x212121称函数 f(x) 在这个区间上是增函数。2. 如果对于属于这个区间的自变量的任意),f(x)都有f(x时,x当x,x,两个值x212121称函数 f(x) 在这个区间上是减函数。一般地,对于给定区间上的函数f(x) : 函数单调性的定义如果函数 f(x) 在某个区间是增函数或减函数,那么就说函数 f(x) 在这个区间具有(严格的)单调性,这一区间叫做 y=f(x) 的单调区间。1 、函数单调性是对于定义域内的某个子区间而言的。2 、理解函数单调性的时候注意三点:① x1 、 x2 是在同一个区间上②任意取的两个实数,③一般都不妨设为一大一小。3 、函数单调性反映的是函数在相应区间上函数值随 x而变化的趋势。 画出反比例函数 的图象。( 1 )这个函数的定义域 I 是什么?( 2 )它在定义域 I 上的单调性是怎样的?证明你的结论。xy1 通过观察图象,先对函数是否具有某种性质做出猜想,然后通过逻辑推理,证明这种猜想的正确性,是研究函数性质的一种常用方法。探究 1: 2( )2练习 判断函数 的 单调性,并加以证明。f xxx单调递增区间:单调递减区间:]1 ,(), 1[xx2x)x(f2 y21o 1( )0f xx 探究2: 证明函数-1在区间(,)上是单调增函数。12 x ,(,0)x 设是区间内任意12121221121111( )()(1)(1)xxf xf xxxxxx x 0x ,2121xxx0)()(21xfxf)()(21xfxf即1( )(,0)f xx 则函数-1在区间证明:。两个实数,且 x 21x...