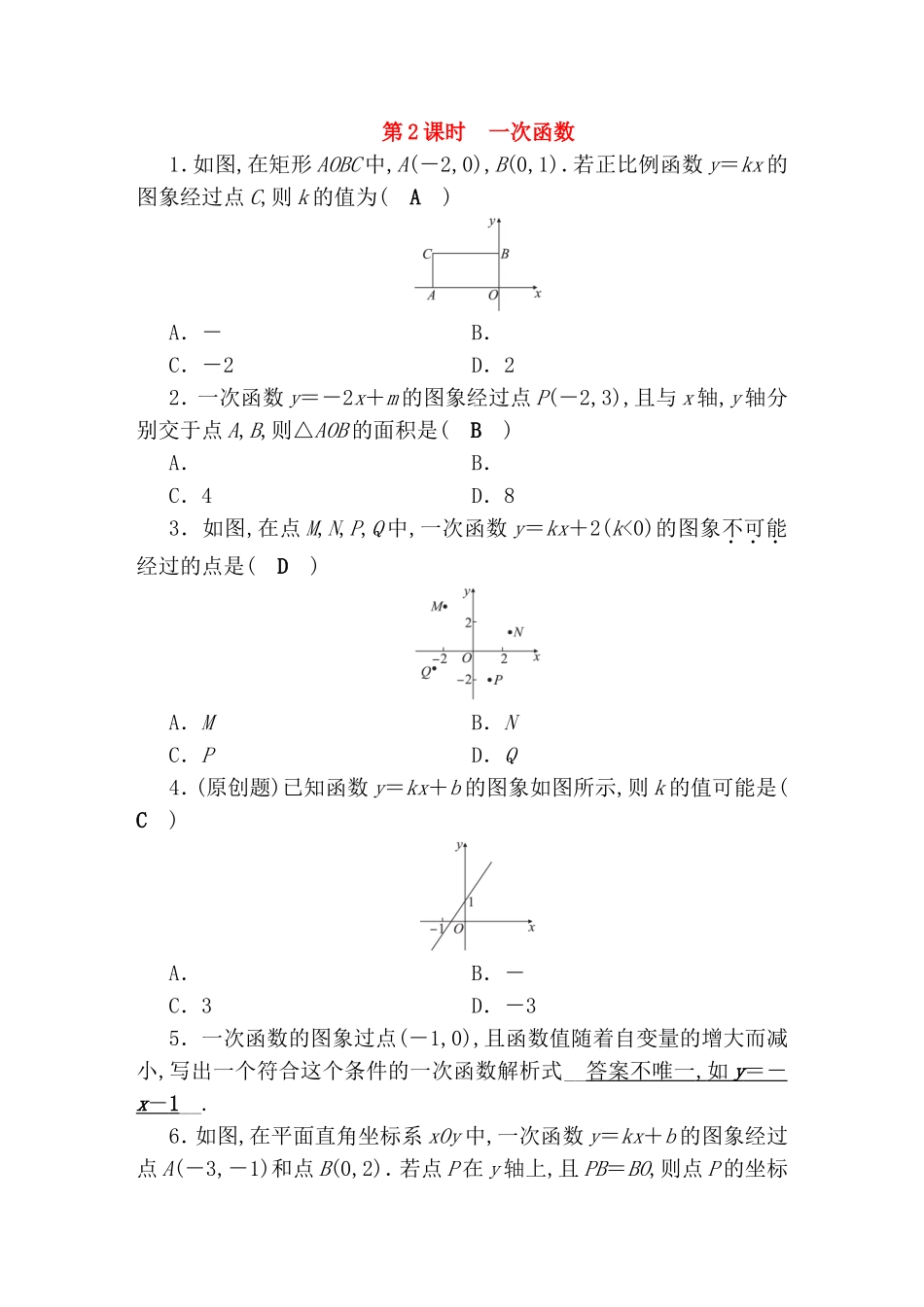
第2课时一次函数1.如图,在矩形AOBC中,A(-2,0),B(0,1).若正比例函数y=kx的图象经过点C,则k的值为(A)A.-B.C.-2D.22.一次函数y=-2x+m的图象经过点P(-2,3),且与x轴,y轴分别交于点A,B,则△AOB的面积是(B)A.B.C.4D.83.如图,在点M,N,P,Q中,一次函数y=kx+2(k<0)的图象不可能经过的点是(D)A.MB.NC.PD.Q4.(原创题)已知函数y=kx+b的图象如图所示,则k的值可能是(C)A.B.-C.3D.-35.一次函数的图象过点(-1,0),且函数值随着自变量的增大而减小,写出一个符合这个条件的一次函数解析式__答案不唯一,如y=-x-1__.6.如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象经过点A(-3,-1)和点B(0,2).若点P在y轴上,且PB=BO,则点P的坐标为__(0,1)或(0,3)__.7.在平面直角坐标系内有两点A,B,其坐标为A(-1,-1),B(2,7),点M为x轴上的一个动点,若要使MB-MA的值最大,则点M的坐标为____.8.在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).(1)当-2<x≤3时,求y的取值范围;(2)已知点P(m,n)在该函数的图象上,且m-n=4,求点P的坐标.解:(1)由题意知y=kx+2,因为图象过点(1,0),∴0=k+2,解得k=-2,∴y=-2x+2.当x=-2时,y=6,当x=3时,y=-4, k=-2<0,∴函数值y随x的增大而减小,∴-4≤y<6;(2)根据题意知解得∴点P的坐标为(2,-2).9.直线l的解析式为y=-2x+2,分别交x轴、y轴于点A,B.(1)写出A,B两点的坐标,并画出直线l的图象;(2)将直线l向上平移4个单位得到l1,l1交x轴于点C.作出l1的图象,l1的解析式是__________;(3)将直线l绕点A顺时针旋转90°得到l2,l2交l1于点D.作出l2的图象,tan∠CAD=__________.解:(1)A(1,0),B(0,2),直线l如图所示;(2)y=-2x+6,直线l1如图所示;(3)直线l2如图所示,tan∠CAD=.10.如图,过点A(2,0)的两条直线l1,l2分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB=.(1)求点B的坐标;(2)若△ABC的面积为4,求直线l2的解析式.解:(1) 点A的坐标为(2,0),∴AO=2.在Rt△AOB中,22+OB2=()2,∴OB=3,∴B(0,3);(2) S△ABC=BC·OA,即4=BC×2,∴BC=4,∴OC=BC-OB=4-3=1,∴C(0,-1).设直线l2的解析式为y=kx+b. 直线l2经过点A(2,0),C(0,-1),∴解得∴直线l2的解析式为y=x-1.11.某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(h)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.(1)当x≥30,求y与x之间的函数关系式;(2)若小李4月份上网20小时,他应付多少元的上网费用?(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?解:(1)当x≥30时,设函数关系式为y=kx+b,则解得所以y=3x-30;(2)4月份上网20小时,应付上网费60元;(3)由75=3x-30解得x=35,所以他在5月份上网35个小时.12.甲、乙两人分别从A,B两地同时出发,匀速相向而行.甲的速度大于乙的速度,甲到达B地后,乙继续前行.设出发xh后,两人相距ykm,图中折线表示从两人出发至乙到达A地的过程中y与x之间的函数关系.根据图中信息,求:(1)点Q的坐标,并说明它的实际意义;(2)甲、乙两人的速度.解:(1)设直线PQ的解析式为y=kx+b,代入点(0,10)和的坐标,得解得故直线PQ的解析式为y=-10x+10,当y=0时,x=1,故点Q的坐标为(1,0),该点表示甲、乙两人经过1小时相遇;(2)由点M的坐标可知甲经过x=h达到B地,故甲的速度为10km÷h=6km/h;设乙的速度为xkm/h,由两人经过1小时相遇,得1·(x+6)=10,解得x=4,故乙的速度为4km/h.13.某村在推进美丽乡村活动中,决定建设幸福广场,计划铺设相同大小规格的红色和蓝色地砖.经过调查,获取信息如下:购买数量低于5000块购买数量不低于5000块红色地砖原价销售以八折销售蓝色地砖原价销售以九折销售如果购买红色地砖4000块,蓝色地砖6000块,需付款86000元;如果购买红色地砖10000块,蓝色地砖3500块,需付款99000元.(1)红色地砖与蓝色地砖的单价各多少元?(2)经过测算,需要购置地砖12000块,其中蓝色地砖的数量不少于红色地砖的一半,并且不超过6000块,如何购买付款最少?请说明理由.解:(1)设红色地砖每块a元,蓝色地砖每块b元.由题意得解得∴红色地砖每块...