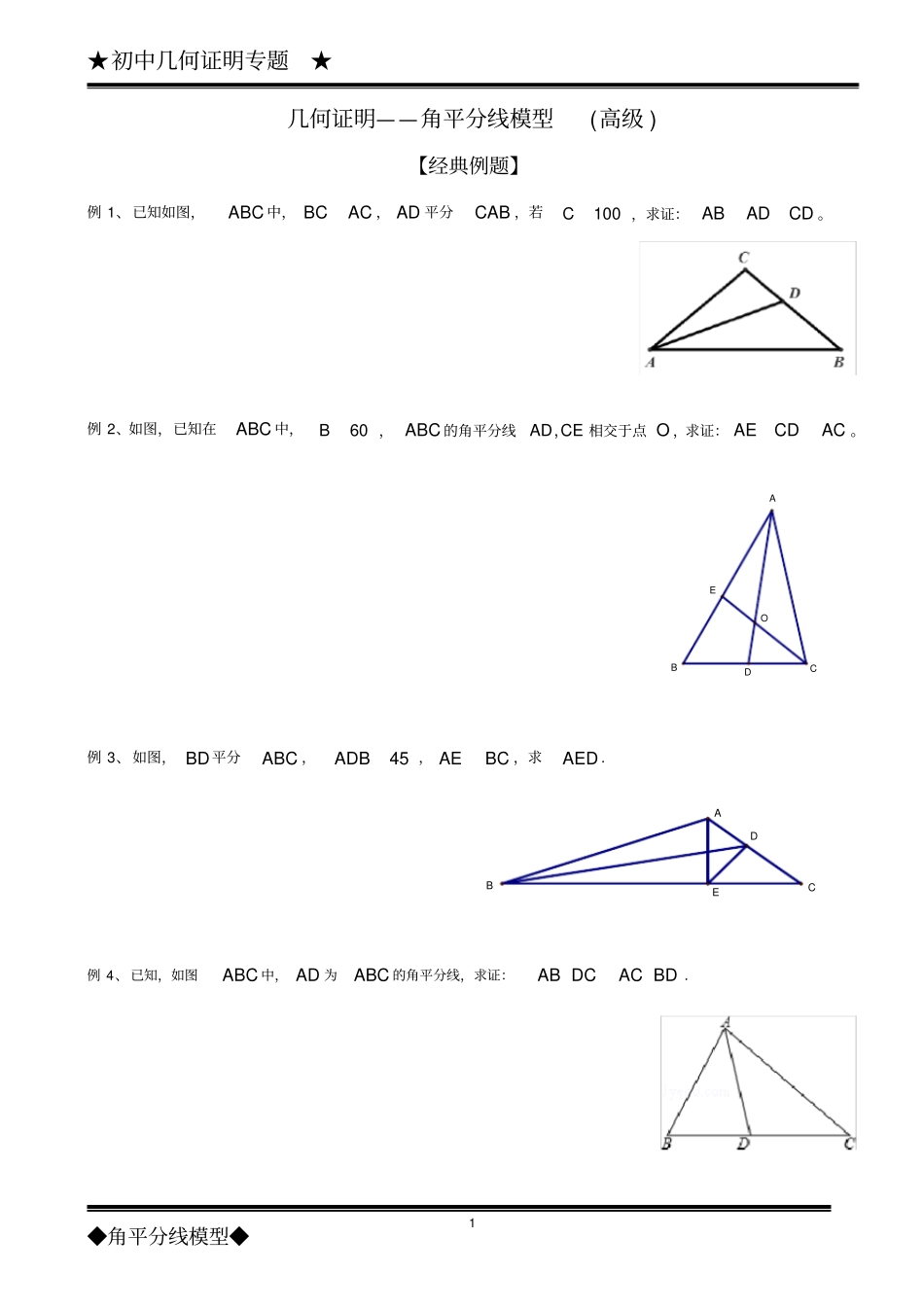
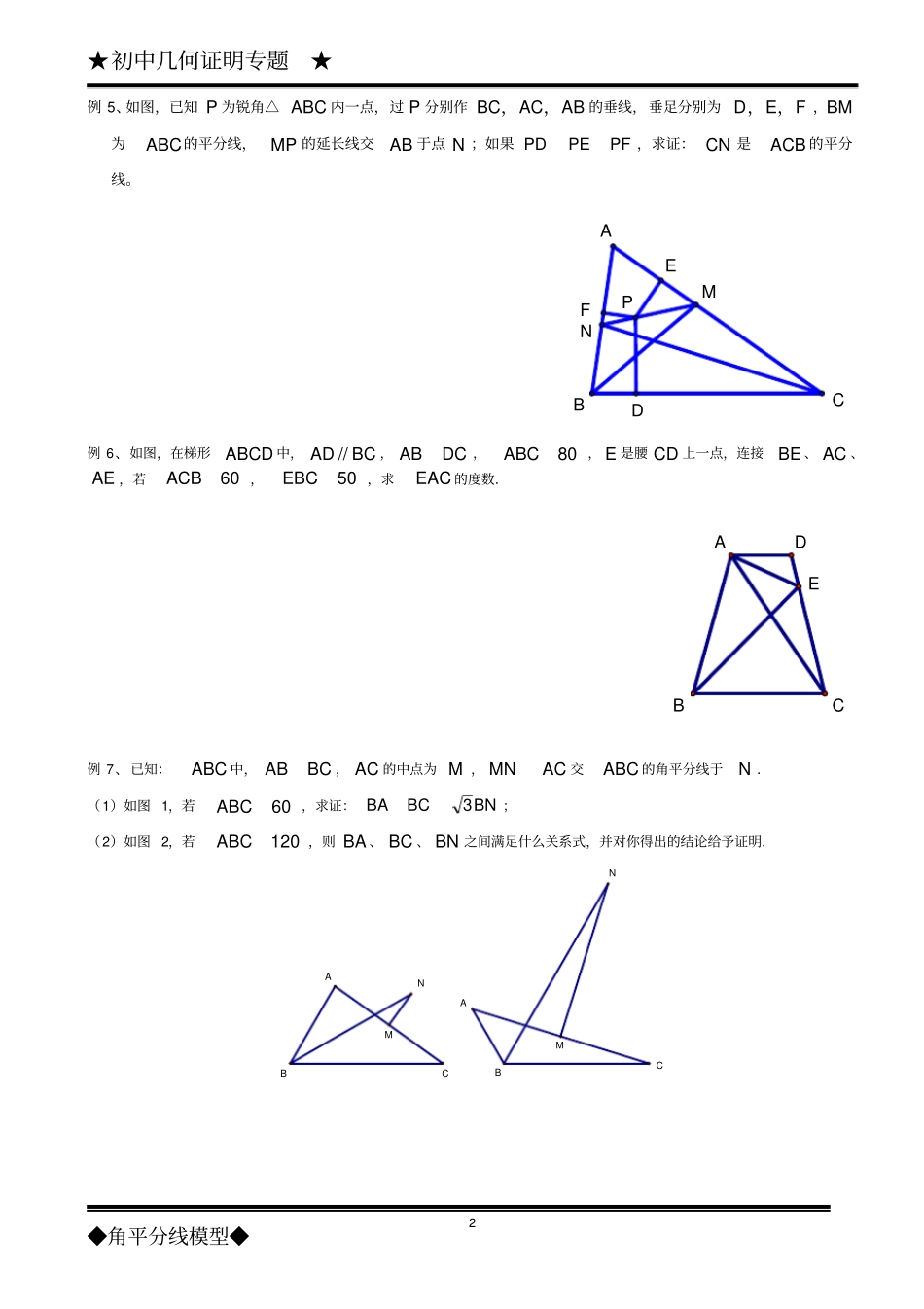
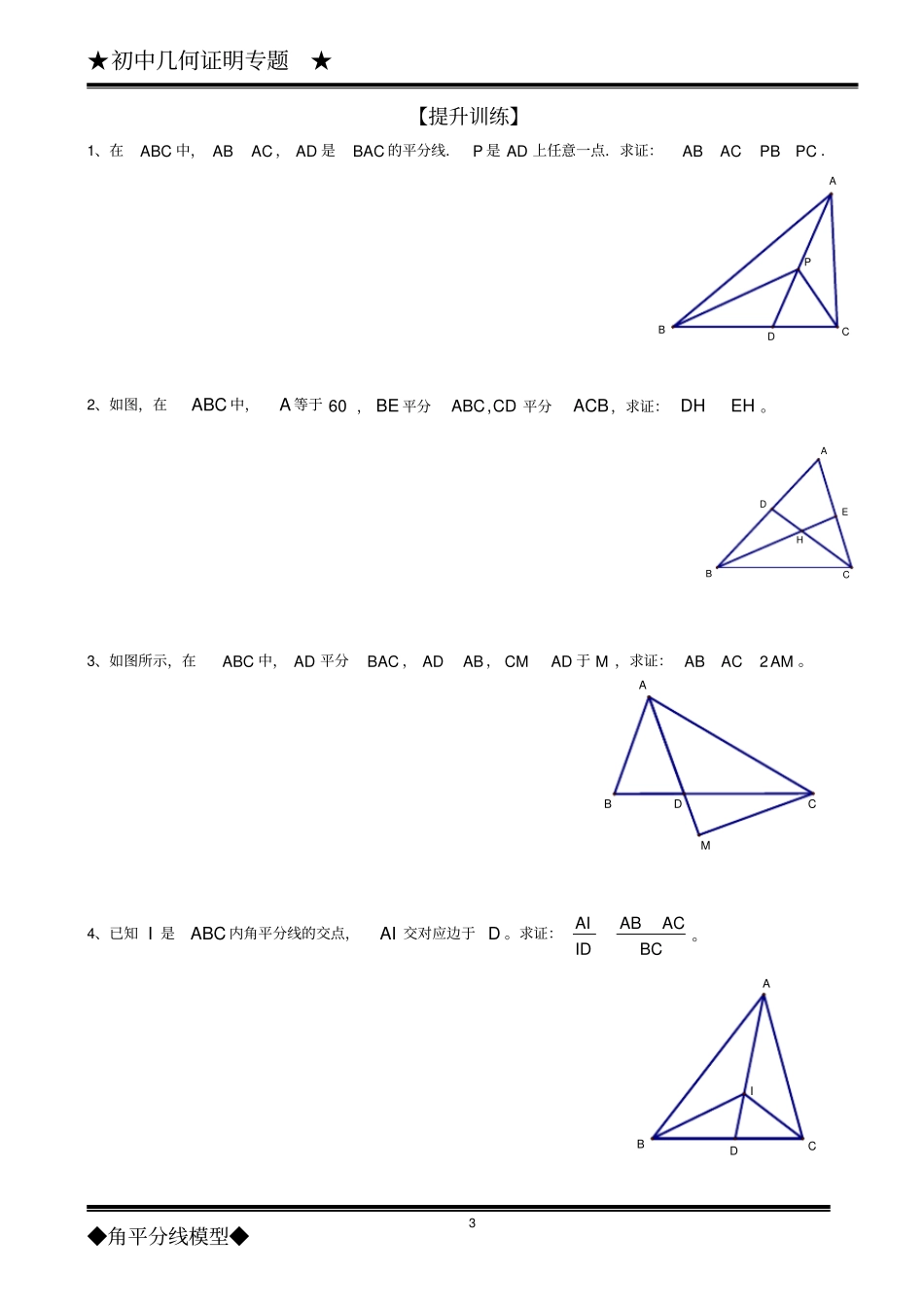
★初中几何证明专题★◆角平分线模型◆1几何证明——角平分线模型(高级)【经典例题】例1、已知如图,ABC中,BCAC,AD平分CAB,若100C,求证:CDADAB。例2、如图,已知在ABC中,60B,ABC的角平分线CEAD,相交于点O,求证:ACCDAE。EDOBCA例3、如图,BD平分ABC,45ADB,BCAE,求AED.EABCD例4、已知,如图ABC中,AD为ABC的角平分线,求证:BDACDCAB.★初中几何证明专题★◆角平分线模型◆2例5、如图,已知P为锐角△ABC内一点,过P分别作ABACBC,,的垂线,垂足分别为FED,,,BM为ABC的平分线,MP的延长线交AB于点N;如果PFPEPD,求证:CN是ACB的平分线。ABCNMPDEF例6、如图,在梯形ABCD中,BCAD//,DCAB,80ABC,E是腰CD上一点,连接BE、AC、AE,若60ACB,50EBC,求EAC的度数.ABCDE例7、已知:ABC中,BCAB,AC的中点为M,ACMN交ABC的角平分线于N.(1)如图1,若60ABC,求证:BNBCBA3;(2)如图2,若120ABC,则BA、BC、BN之间满足什么关系式,并对你得出的结论给予证明.NMANMBACBC★初中几何证明专题★◆角平分线模型◆3【提升训练】1、在ABC中,ABAC,AD是BAC的平分线.P是AD上任意一点.求证:ABACPBPC.DBCAP2、如图,在ABC中,A等于60,BE平分CDABC,平分ACB,求证:EHDH。EHDCBA3、如图所示,在ABC中,AD平分BAC,ADAB,CMAD于M,求证:2ABACAM。MCABD4、已知I是ABC内角平分线的交点,AI交对应边于D。求证:BCACABIDAI。DIABC★初中几何证明专题★◆角平分线模型◆45、(1)如图,BD、CE分别是ABC的外角平分线,过点A作BDAF,CEAG,垂足分别为F、G,连接FG,延长AF、AG,与直线BC相交,求证:ACBCABFG21。(2)若BD、CE分别是ABC的内角平分线(如图(2)),过点A作BDAF,CEAG,垂足分别为F、G,连接FG,线段FG与ABC三边有怎样的数量关系?;(3)若BD为ABC的内角平分线,CE为ABC的外角平分线(如图(3)),过点A作BDAF,CEAG,垂足分别为F、G,连接FG,则线段FG与ABC三边又有怎样的数量关系?(3)(2)(1)DGFDEGFFGABCAADEBCBCE6、如图,已知BD,CE为ABC的角平分钱,F为DE的中点,点F到AC,AB,BC的距离分别为aFG,bFH,cFM,若025221222mmabcc。(1)求a,b,c,m的值;(2)求证:)(41CDBCDG。ABCEDFMHG★初中几何证明专题★◆角平分线模型◆57.已知如图,CD是ABCRt斜边上的高,A的平分线交CD于H,交BCD的平分线于G,求证:BCHF//.8.如图,BD、CE为△ABC的两条内角平分线,K为ED的中点,KF⊥AB于F,KG⊥AC于G,KH⊥BC于H,求证:KF+KG=KH.9.已知BCAC,90ACB,15DCB,CDBD,ADCE于点E,求证:CEBC2.10.(1)如图1,BP为△ABC的角平分线,PM⊥AB于M,PN⊥BC于N,AB=30,BC=23,请补全图形,并求△ABP与△BPC的面积的比值;(2)如图2,分别以△ABC的边AB、AC为边向外作等边三角形ABD和等边三角形ACE,CD与BE相交于点O,判断∠AOD与∠AOE的数量关系,并证明;(3)在四边形ABCD中,已知BC=DC,且AB≠AD,对角线AC平分∠BAD,请直接写出∠B和∠D的数量关系.★初中几何证明专题★◆角平分线模型◆611.(1)已知:如图1,Rt△ABC中,∠ACB=90°,∠BAC=60°,CD平分∠ACB,点E为AB中点,PE⊥AB交CD的延长线于P,猜想:∠PAC+∠PBC=°(直接写出结论,不需证明).(2)已知:如图2,Rt△ABC中,∠ACB=90°,∠BAC≠45°,CD平分∠ACB,点E为AB中点,PE⊥AB交CD的延长线于P,(1)中结论是否成立,若成立,请证明;若不成立请说明理由.12.如图1,分别过线段AB的端点A、B作直线AM、BN,且AM∥BN,∠MAB、∠NBA的角平分线交于点C,过点C的直线l分别交AM、BN于点D、E.(1)求证:△ABC是直角三角形;(2)在图1中,当直线l⊥AM时,线段AD、BE、AB之间有怎样的数量关系?证明你的猜想;(3)当直线l绕点C旋转到与AM不垂直时,在如图2、3两种情况下,(2)中的三条线段之间又有怎样的数量关系?请写出你的猜想,并选择一种情况给予证明.13.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠BAC,交CD于K,交BC于E,F是BE上一点,且BF=CE,求证:FK∥AB.★初中几何证明专题★◆角平分线模型◆714.在ABC中,AD是∠BAC的平分线.(1)如图①,求证:ACABSSACDABD;(2...