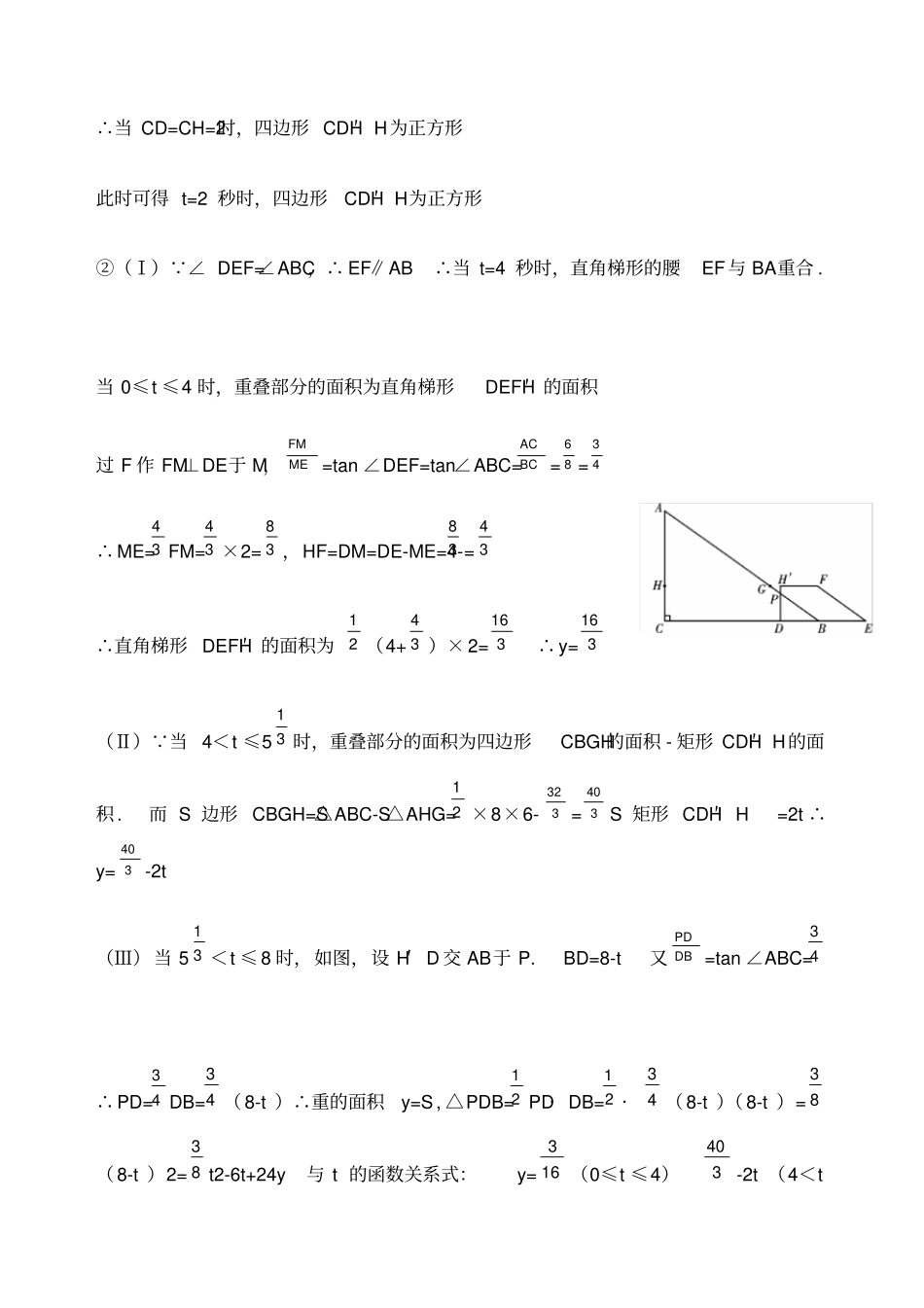
中考压轴动点问题1、如图11,在△ABC中,∠C=90°,BC=8,AC=6,另有一直角梯形DEFH(HF∥DE,∠HDE=90°)的底边DE落在CB上,腰DH落在CA上,且DE=4,∠DEF=∠CBA,AH∶AC=2∶3(1)延长HF交AB于G,求△AHG的面积.(2)操作:固定△ABC,将直角梯形DEFH以每秒1个单位的速度沿CB方向向右移动,直到点D与点B重合时停止,设运动的时间为t秒,运动后的直角梯形为DEFH′(如图12).探究1:在运动中,四边形CDH′H能否为正方形?若能,解:(1) AH∶AC=2∶3,AC=6∴AH=23AC=23×6=4又 HF∥DE,∴HG∥CB,∴△AHG∽△ACB⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分∴AHAC=HGBC,即46=8HG,∴HG=163∴S△AHG=12AH·HG=12×4×163=323(2)①能为正方形 HH′∥CD,HC∥H′D,∴四边形CDH′H为平行四边形又∠C=90°,∴四边形CDH′H为矩形又CH=AC-AH=6-4=2∴当CD=CH=2时,四边形CDH′H为正方形此时可得t=2秒时,四边形CDH′H为正方形②(Ⅰ) ∠DEF=∠ABC,∴EF∥AB∴当t=4秒时,直角梯形的腰EF与BA重合.当0≤t≤4时,重叠部分的面积为直角梯形DEFH′的面积过F作FM⊥DE于M,FMME=tan∠DEF=tan∠ABC=ACBC=68=34∴ME=43FM=43×2=83,HF=DM=DE-ME=4-83=43∴直角梯形DEFH′的面积为12(4+43)×2=163∴y=163(Ⅱ) 当4<t≤513时,重叠部分的面积为四边形CBGH的面积-矩形CDH′H的面积.而S边形CBGH=S△ABC-S△AHG=12×8×6-323=403S矩形CDH′H=2t∴y=403-2t(Ⅲ)当513<t≤8时,如图,设H′D交AB于P.BD=8-t又PDDB=tan∠ABC=34∴PD=34DB=34(8-t)∴重的面积y=S,△PDB=12PD·DB=12·34(8-t)(8-t)=38(8-t)2=38t2-6t+24y与t的函数关系式:y=316(0≤t≤4)403-2t(4<t≤513)38t2-6t+24(513<t≤8)2、已知直角梯形纸片OABC在平面直角坐标系中的位置如图所示,四个顶点的坐标分别为O(0,0),A(10,0),B(8,32),C(0,32),点T在线段OA上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;(1)求∠OAB的度数,并求当点A′在线段AB上时,S关于t的函数关系式;(2)当纸片重叠部分的图形是四边形时,求t的取值范围;(3)S存在最大值吗?若存在,求出这个最大值,并求此时t的值;若不存在,请说明理由.(1) A,B两点的坐标分别是A(10,0)和B(8,32),(2)∴381032OABtan,∴60OAB当点A′在线段AB上时, 60OAB,TA=TA′,∴△A′TA是等边三角形,且ATTP,∴)t10(2360sin)t10(TP,)t10(21AT21APPA,当6t2时,由图,重叠部分的面积EBATPASSS △A′EB的高是60sinBA,∴23)4t10(21)t10(83S2234)2t(83)28t4t(8322当t=2时,S的值最大是34;当2t0,即当点A′和点P都在线段AB的延长线是(如图,其中E是TA′与CB的交点,F是TP与CB的交点), ETFFTPEFT,四边形ETAB是等腰形,∴EF=ET=AB=4,∴3432421OCEF21S综上所述,S的最大值是34,此时t的值是2t0.3、如图(1)在Rt△ACB中,∠C=90°AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ。若设运动的时间为t(s)(0<t<2).根据以上信息,解答下列问题:(1)当t为何值时,以A、P、Q为顶点的三角形与△ABC相似?(2)设四边形PQCB的面积为y(),直接写出y与t之间的函数关系式;(3)在点P、点Q的移动过程中,如果将△APQ沿其一边所在直线翻折,翻折后的三角形与△APQ组成一个四边形,那么是否存在某一时刻t,使组成的四边形为菱形?若存在,求出t的值;若不存在,请说明理由.------------2分(2)???????????????③当沿AQ翻折时,PQ=AP,过P点作PH⊥AC于H,则点H必为AQ的中点,∴Rt△AHP∽Rt△ACB,∴即,解得:>2(不合题意应舍去)综上所述,当时,所形成的四边形为菱形.-------------------4.如图24-1,在ABC△中,90Ao,4AB,3AC.M是边AB上的动点(M不与AB,重合),MNBC∥交AC于点N,AMN△关于MN的对称图形是PMN△.设AMx.(1)用含x的式子表示AMN△的面积(不必写出过程);(2)当x为何值时,点P恰好落在边BC上;(3)在动点M的运动过程中,记PMN△与梯形MBCN重叠部分的面积为y,...