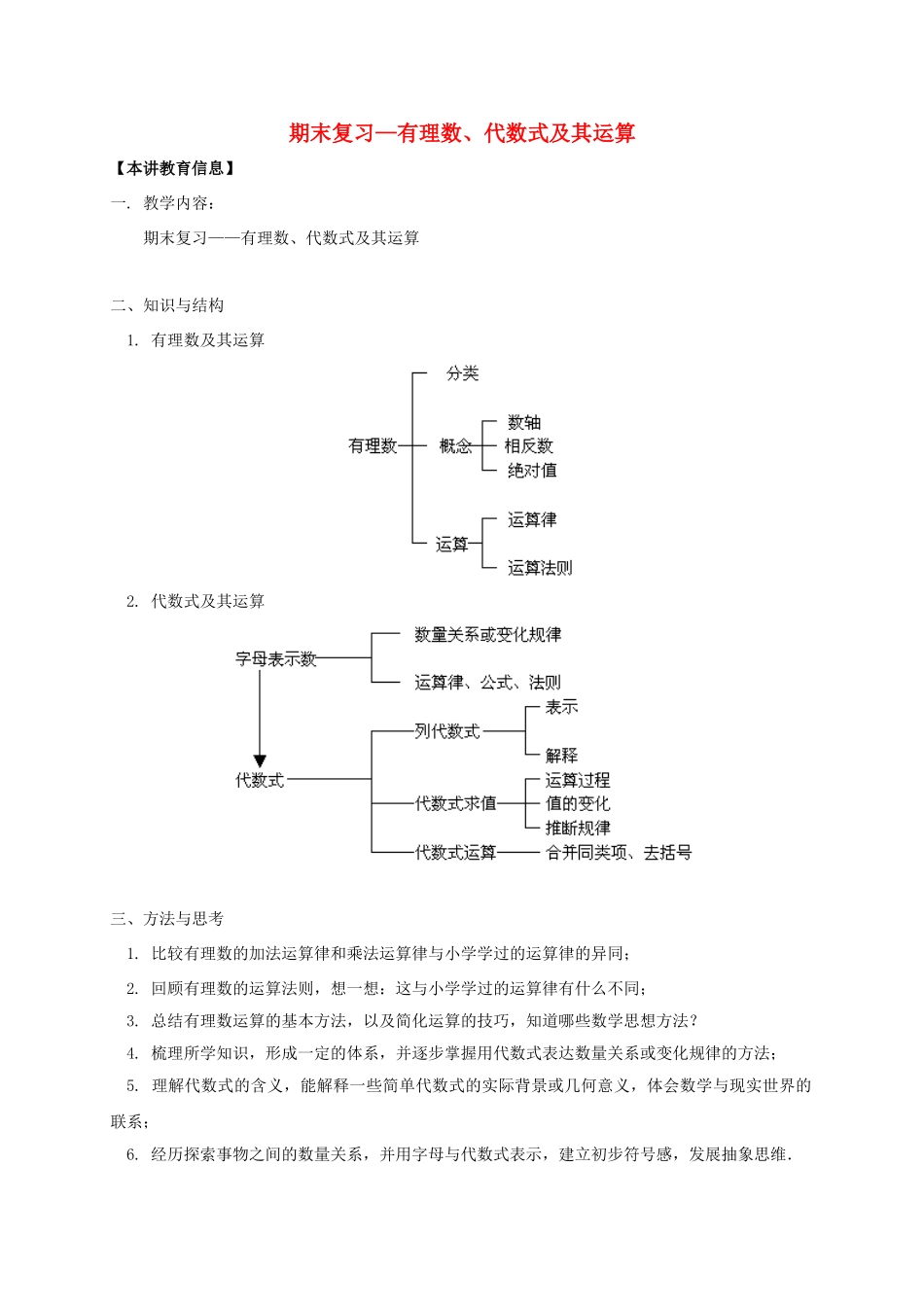
期末复习—有理数、代数式及其运算【本讲教育信息】一.教学内容:期末复习——有理数、代数式及其运算二、知识与结构1.有理数及其运算2.代数式及其运算三、方法与思考1.比较有理数的加法运算律和乘法运算律与小学学过的运算律的异同;2.回顾有理数的运算法则,想一想:这与小学学过的运算律有什么不同;3.总结有理数运算的基本方法,以及简化运算的技巧,知道哪些数学思想方法?4.梳理所学知识,形成一定的体系,并逐步掌握用代数式表达数量关系或变化规律的方法;5.理解代数式的含义,能解释一些简单代数式的实际背景或几何意义,体会数学与现实世界的联系;6.经历探索事物之间的数量关系,并用字母与代数式表示,建立初步符号感,发展抽象思维.四、错题回放1.代数式书写规范.如a的倍写成a,应为.2.代数式描述语句顺序不理解.如a,b两数的平方和写成,应为.3.合并同类项中出错.如,.4.去括号中符号出错.如,.5.探索规律出错.如由1+3=4=22,1+3+5=9=32,1+3+5+7=16=42,1+3+5+7+9=25=52,…猜想1+3+5+7+…+(2n+1)=n2(n为正整数)【典型例题】例1.如图,在数轴上有三个点A、B、C,回答下列问题:(1)将B点向右移动6个单位,三个点中哪个点所表示的数最小?(2)将C点向左移动6个单位,三个点中哪个点所表示的数最小?(3)怎样移动A、B、C中两个点,才能使三个点所表示的数相同?有几种移动方法?分析:注意移动的方向及相关点所对应的有理数.解:(1)B点向右移动6个单位就为-1+6=5,所以三个点中A点-2最小;(2)C点向左移动6个单位就为2-6=-4,所以三个点中C点-4最小;(3)有三种方法:①将B点向左移动1个单位;将C点向左移动4个单位;则三个数都为-2②将A点向右移动1个单位;将C点向左移动3个单位;则三个数都为-1③将A点向右移动4个单位;将B点向右移动3个单位;则三个数都为2例2.有理数a、b、c在数轴上的位置如图所示,其中O是原点,=.(1)用“<”把a、b、-a、-b连接起来;(2)b+c的值是多少?(3)判断a+b与a+c的符号.分析:比较a、b、-a、-b的大小时,可根据互为相反数的两个数在原点两侧,并且到原点的距离相等这一原理,在数轴上画出表示-a、-b的两点,即可得它们的大小关系.解:(1)a