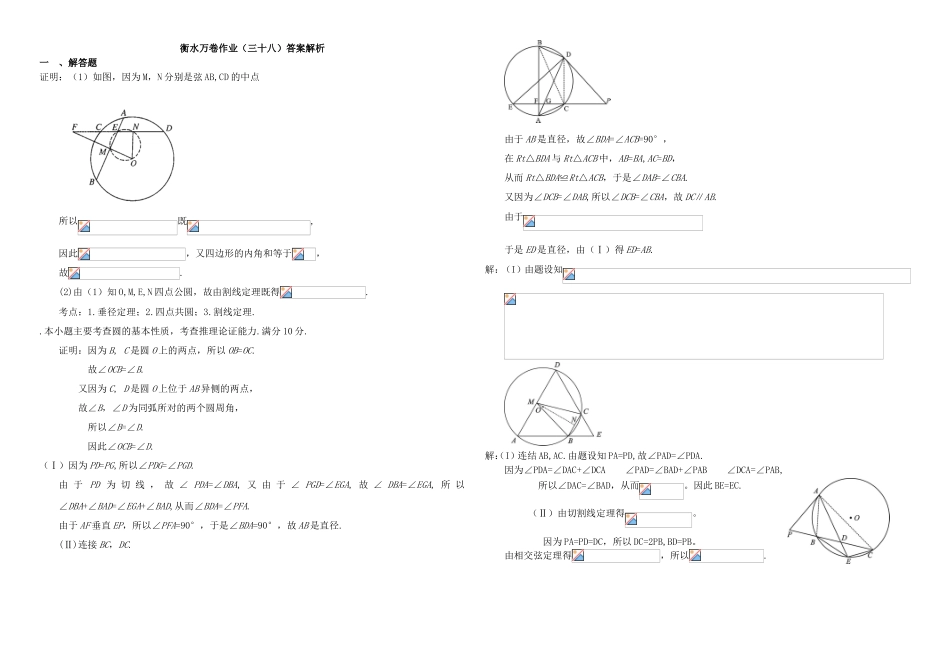
衡水万卷作业(三十八)几何证明考试时间:45分钟姓名:__________班级:__________考号:__________一、解答题(本大题共5小题,共100分)如图,在圆O中,相交于点E的两弦AB、CD的中点分别是M、N,直线MO与直线CD相交于点F,证明:(1);(2)【选修4-1:几何证明选讲】如图,AB是圆O的直径,C、D是圆O上位于AB异侧的两点证明:∠OCB=∠D.选修4-1:几何证明选讲如图,EP交圆于E、C两点,PD切圆于D,G为CE上一点且,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.(1)求证:AB为圆的直径;(2)若AC=BD,求证:AB=ED.选修4—1:几何证明选讲如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE(Ⅰ)证明:∠D=∠E;(Ⅱ)设AD不是⊙O的直径,AD的中点为M,且MB=MC,证明:△ADE为等边三角形.选修4—1:几何证明选讲如图,P是O外一点,PA是切线,A为切点,割线PBC与O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交O于点E.证明:(Ⅰ)BE=EC;(Ⅱ)ADDE=2衡水万卷作业(三十八)答案解析一、解答题证明:(1)如图,因为M,N分别是弦AB,CD的中点所以既,因此,又四边形的内角和等于,故.(2)由(1)知O,M,E,N四点公圆,故由割线定理既得.考点:1.垂径定理;2.四点共圆;3.割线定理..本小题主要考查圆的基本性质,考查推理论证能力.满分10分.证明:因为B,C是圆O上的两点,所以OB=OC.故∠OCB=∠B.又因为C,D是圆O上位于AB异侧的两点,故∠B,∠D为同弧所对的两个圆周角,所以∠B=∠D.因此∠OCB=∠D.(Ⅰ)因为PD=PG,所以∠PDG=∠PGD.由于PD为切线,故∠PDA=∠DBA,又由于∠PGD=∠EGA,故∠DBA=∠EGA,所以∠DBA+∠BAD=∠EGA+∠BAD,从而∠BDA=∠PFA.由于AF垂直EP,所以∠PFA=90°,于是∠BDA=90°,故AB是直径.(Ⅱ)连接BC,DC.由于AB是直径,故∠BDA=∠ACB=90°,在Rt△BDA与Rt△ACB中,AB=BA,AC=BD,从而Rt△BDA≌Rt△ACB,于是∠DAB=∠CBA.又因为∠DCB=∠DAB,所以∠DCB=∠CBA,故DC∥AB.由于于是ED是直径,由(Ⅰ)得ED=AB.解:(I)由题设知解:(I)连结AB,AC.由题设知PA=PD,故∠PAD=∠PDA.因为∠PDA=∠DAC+∠DCA∠PAD=∠BAD+∠PAB∠DCA=∠PAB,所以∠DAC=∠BAD,从而。因此BE=EC.(Ⅱ)由切割线定理得。因为PA=PD=DC,所以DC=2PB,BD=PB。由相交弦定理得,所以.