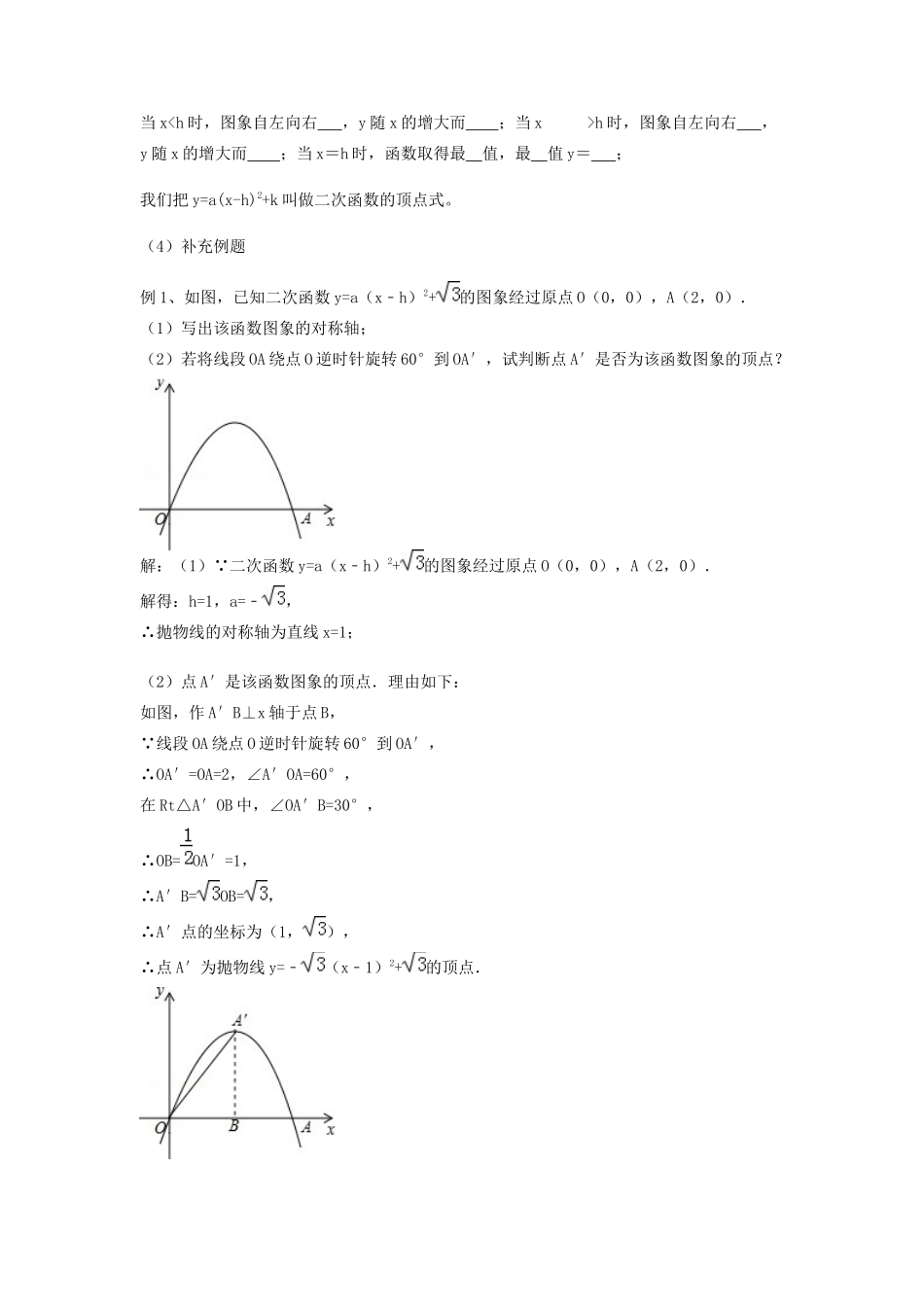
26.2.2二次函数y=a(x-h)2+k的图象及性质教学内容:课本P15~16教学目标:1、会用描点法画出二次函数y=a(x-h)2+k的图象,结合图象说出它的性质;2、会用平移法画二次函数y=a(x-h)2+k的简图,并理解它与二次函数y=ax2的关系。教学重点和难点重点:会用描点法画出二次函数y=a(x-h)2+k的图象,结合图象说出它的性质;难点:会用平移法画二次函数y=a(x-h)2+k的简图,并理解它与二次函数y=ax2的关系。教学准备:课件教学方法:操作体验法教学过程一、复习与练习1、画出二次函数y=-3(x-2)2+1的简图,并说出它的性质;2、已知二次函数y=2x2-3mx-m+5与X轴只有一个交点,求二次函数的对称轴和顶点坐标。二、新课学习(一)学习试一试1、填写下表:2、利用平移法画出二次函数的简图3、写出二次函数的性质(1)二次函数的图象是一条;它开口,关于对称,顶点坐标是。(2)函数的图象是函数的图象向上平移单位,再向右平移单位长度。(3)当x<2时,图象从左到右,y随x的增大而。当x>2时,图象从左到右,y随x的增大而。(4)顶点是图象的最点,因此,当x=2时,函数取得最小值,最小值y=.(二)学习做一做1、画出函数的简图,说出它的性质;2、画出函数的简图,说出它的性质;(三)概括:二次函数y=a(x-h)2+k的图象与性质(1)二次函数y=a(x-h)2+k的图象是一条,它关于对称,顶点坐标是;(2)二次函数yy=a(x-h)2+k的图象是函数y=ax2的图象沿x轴平移单位,再沿Y轴平移单位长度。(3)当a>0时,抛物线的开口向,图象在第象限,顶点是最点;当xh时,图象自左向右,y随x的增大而;当x=h时,函数取得最值,最值y=;当a<0时,抛物线的开口向,图象在第象限,顶点是最点;当xh时,图象自左向右,y随x的增大而;当x=h时,函数取得最值,最值y=;我们把y=a(x-h)2+k叫做二次函数的顶点式。(4)补充例题例1、如图,已知二次函数y=a(x﹣h)2+的图象经过原点O(0,0),A(2,0).(1)写出该函数图象的对称轴;(2)若将线段OA绕点O逆时针旋转60°到OA′,试判断点A′是否为该函数图象的顶点?解:(1)∵二次函数y=a(x﹣h)2+的图象经过原点O(0,0),A(2,0).解得:h=1,a=﹣,∴抛物线的对称轴为直线x=1;(2)点A′是该函数图象的顶点.理由如下:如图,作A′B⊥x轴于点B,∵线段OA绕点O逆时针旋转60°到OA′,∴OA′=OA=2,∠A′OA=60°,在Rt△A′OB中,∠OA′B=30°,∴OB=OA′=1,∴A′B=OB=,∴A′点的坐标为(1,),∴点A′为抛物线y=﹣(x﹣1)2+的顶点.例2、抛物线y=ax2+bx+c(a≠0)向右平移2个单位得到抛物线y=a(x﹣3)2﹣1,且平移后的抛物线经过点A(2,1).(1)求平移后抛物线的解析式;(2)设原抛物线与y轴的交点为B,顶点为P,平移后抛物线的对称轴与x轴交于点M,求△BPM的面积.解:(1)把点A(2,1)代入y=a(x﹣3)2﹣1,得1=a(2﹣3)2﹣1,整理,得1=a﹣1,解得a=2.则平移后的抛物线解析式为:y=2(x﹣3)2﹣1;(2)由(1)知,平移后的抛物线解析式为:y=2(x﹣3)2﹣1,则M(3,0)∵抛物线y=ax2+bx+c(a≠0)向右平移2个单位得到抛物线y=2(x﹣3)2﹣1,∴平移前的抛物线解析式为:y=2(x﹣1)2﹣1.∴P(1,﹣1).令x=0,则y=1.故B(0,1),∴BM=∴S△BPM=BM•yP=××1=.练习:课本P16页第1.2.3补充练习1、将二次函数y=x2的图象向下平移1个单位,再向右平移1个单位后所得图象的函数表达式为()A.y=(x+1)2+1B.y=(x+1)2﹣1C.y=(x﹣1)2+1D.y=(x﹣1)2﹣12.将抛物线y=(x﹣1)2向左平移2个单位,所得抛物线的表达式为()A.y=(x+1)2B.y=(x﹣3)2C.y=(x﹣1)2+2D.y=(x﹣1)2﹣23、抛物线y=x2+2向左平移2个单位得到的抛物线表达式为_________.三、小结1、学生总结2、老师总结:本节课学习了二次函数y=a(x-h)2+k的图象与性质四、布置作业1、课本P24,习题26.2第1题。2、课本P33,复习题第8、9题。五、板书设计26.2.2二次函数y=a(x-h)2+k的图象与性质一、复习与练习二、学习试一试三、概括四、补充例题六、反思