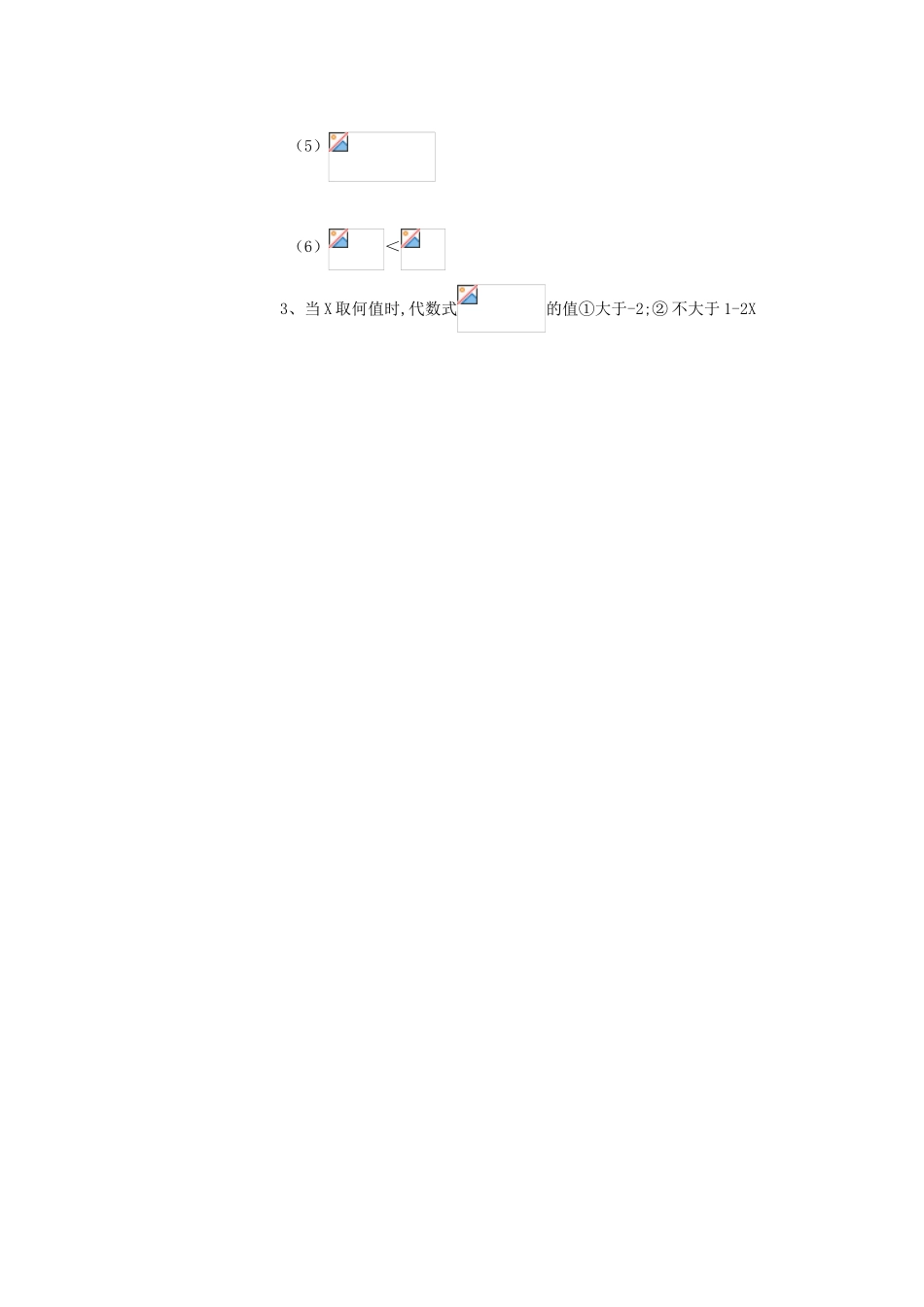
第四课时解一元一次不等式①一、教学目标:(1)使学生掌握一元一次不等式的概念及其标准形式;(2)用解一元一次方程的步骤来探索解一元一次不等式的一般步骤;(3)会解一元一次不等式,重视数学学习中转化思想的运用。二、复习练习:1.复习提问:(1)不等式的三条基本性质是什么?(2)运用不等式基本性质把下列不等式化成的形式.①②③④(3)什么叫一元一次方程?解一元一次方程的步骤是什么?三、新课探究:1.一元一次不等式的定义:只含有一个未知数,且含未知数的式子是整式,未知数的次数是1.像这样的不等式叫做一元一次不等式.2.一元一次不等式的标准形式是:.3.求一元一次不等式解集的过程叫解一元一次不等式.4.解一元一次不等式就是把不等式化成的形式.四、基础例解:例1、解下列不等式,并将解集在数轴上表示出来:⑴⑵例2、⑴解一元一次方程,并说说经过哪些步骤。⑵请你将⑴中方程改为一元一次不等式,并解此不等式。⑶比较⑴与⑵,请你与同学互相讨论,归纳解一元一次方程与解一元一次不等式方法、步骤的异同点,并合作填写下表。解一元一次方程解一元一次不等式相同步骤区别学生练习:课本P62练习1、2.例3、解下列不等式,并将解集在数轴上表示出来:①②五、能力拓展:例4、取何值时,代数式的值①大于的值;②不大于的值;③是非负数;④不小于3.例5、求同时满足和的整数解.六、延伸与提高:例6、①代数式的值小于3且大于0,求x的取值范围.②、有一本书,共300页,前5天读了100页,现要在10天内(包括第10天)读完,则从第6天起每天至少读多少页?七、课时小结:⑴一元一次不等式的定义;⑵解一元一次不等式的注意点:①移项要变号(同方程解法)②当不等式两边都乘以或除以一个负数时,不等号方向改变.八、课时作业:1、解下列不等式:(1)3x+2<2x—5(2)≥—2(3)3(y+2)—1≥8—2(y—1)(4)<1(5)>(6)≤2、解下列不等式,并将解集在数轴上表示出来:(1)3x+2<2x—8(2)3—2x≥9+4x(3)2(2x+3)<5(x+1)(4)19—3(x+7)≤0(5)(6)<3、当X取何值时,代数式的值①大于-2;②不大于1-2X