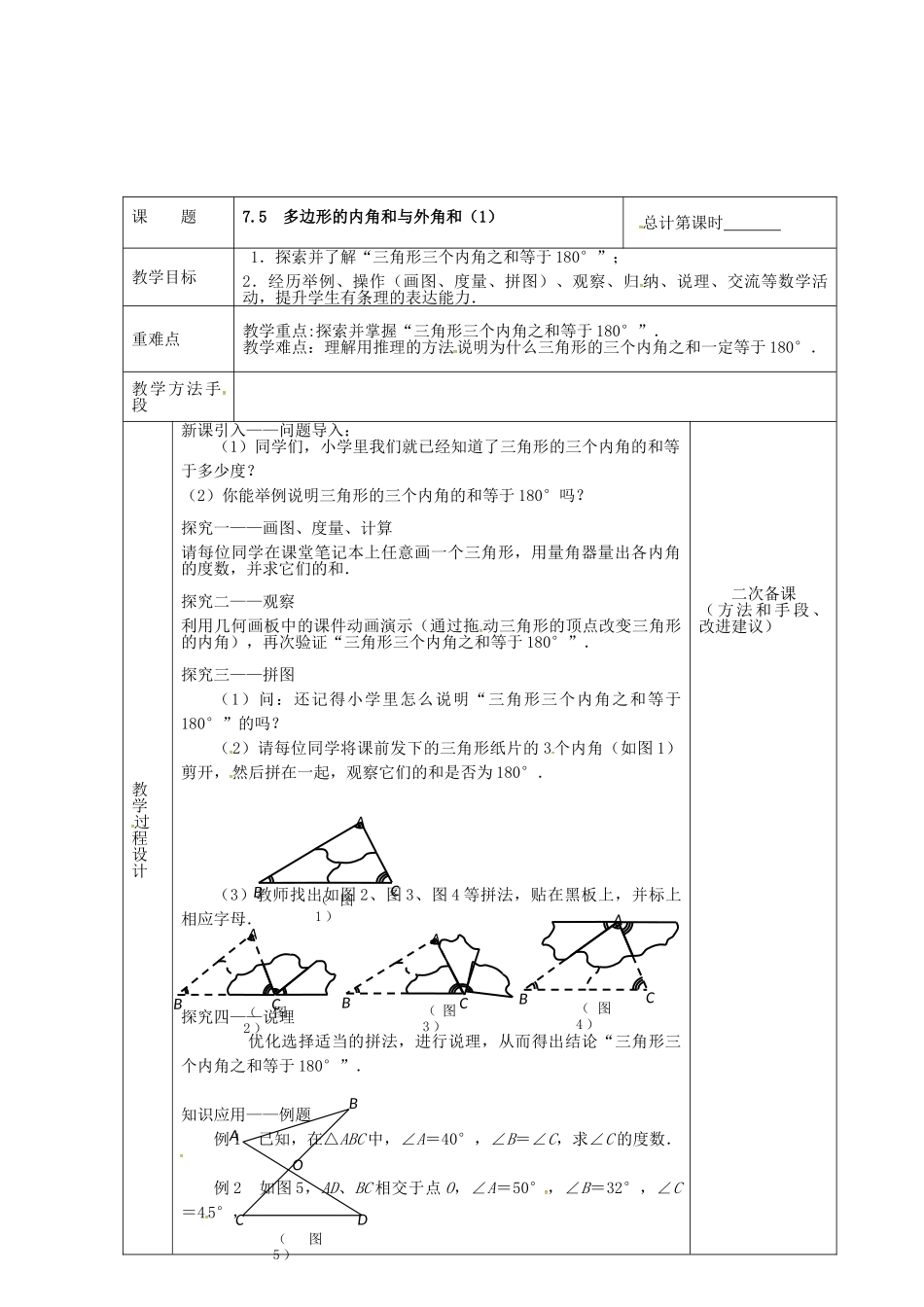
7.5多边形的内角和与外角和课题7.5多边形的内角和与外角和(1)总计第课时教学目标1.探索并了解“三角形三个内角之和等于180°”;2.经历举例、操作(画图、度量、拼图)、观察、归纳、说理、交流等数学活动,提升学生有条理的表达能力.重难点教学重点:探索并掌握“三角形三个内角之和等于180°”.教学难点:理解用推理的方法说明为什么三角形的三个内角之和一定等于180°.教学方法手段教学过程设计新课引入——问题导入:(1)同学们,小学里我们就已经知道了三角形的三个内角的和等于多少度?(2)你能举例说明三角形的三个内角的和等于180°吗?探究一——画图、度量、计算请每位同学在课堂笔记本上任意画一个三角形,用量角器量出各内角的度数,并求它们的和.探究二——观察利用几何画板中的课件动画演示(通过拖动三角形的顶点改变三角形的内角),再次验证“三角形三个内角之和等于180°”.探究三——拼图(1)问:还记得小学里怎么说明“三角形三个内角之和等于180°”的吗?(2)请每位同学将课前发下的三角形纸片的3个内角(如图1)剪开,然后拼在一起,观察它们的和是否为180°.(3)教师找出如图2、图3、图4等拼法,贴在黑板上,并标上相应字母.探究四——说理优化选择适当的拼法,进行说理,从而得出结论“三角形三个内角之和等于180°”.知识应用——例题例1已知,在△ABC中,∠A=40°,∠B=∠C,求∠C的度数.例2如图5,AD、BC相交于点O,∠A=50°,∠B=32°,∠C=45°,二次备课(方法和手段、改进建议)ABC(图1)ABC(图4)(图3)ABCABC(图2)ABCDO(图5)知识应用——练习1.在△ABC中,若∠A+∠B=90°,则△ABC一定是__________三角形.2.在△ABC中,若∠A∶∠B∶∠C=2∶3∶4,求∠A、∠B、∠C的度数.作业设计教学反思