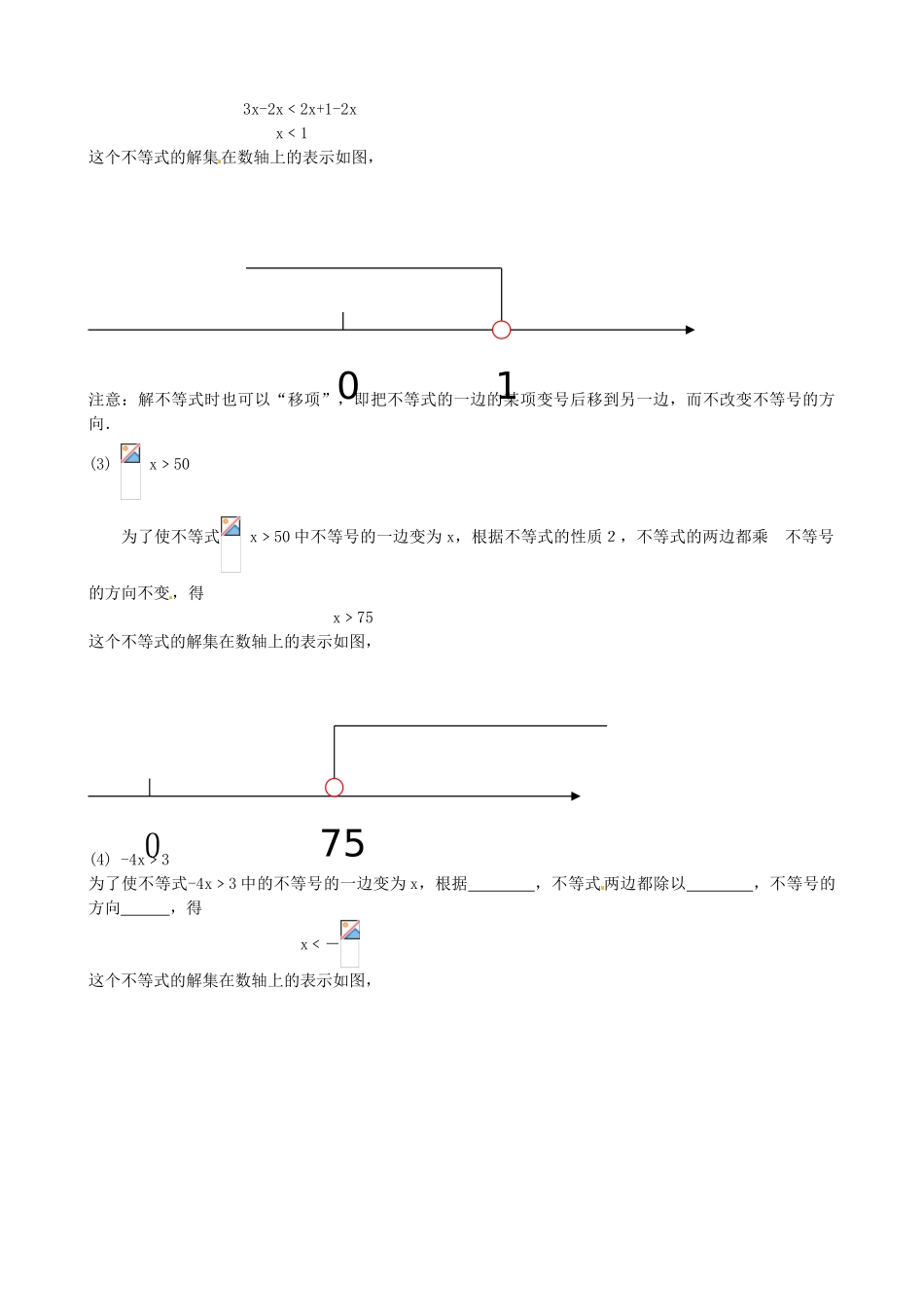
《不等式的性质》教学设计一、教学内容:不等式的性质(人民教育出版社,义务教育课程标准实验教科书七年级下册P123页至P126页)二、教学目标:1.知识技能:①理解不等式的性质;②会解简单的一元一次不等式,并能在数轴上表示出解集;2.数学思考:通过类比等式的性质,探索不等式的性质,体会不等式与等式的异同,初步掌握类比的思想方法;3.解决问题:①通过经历不等式性质的得出过程,积累数学活动经验;②通过分组活动,探索不等式的性质,体会在解决问题过程中与他人合作的重要性;4.情感态度:①认识到通过观察、实验、类比可以获得数学结论,体验数学活动充满着探索性和创造性;②在独立思考的基础上,积极参与对数学问题的讨论,敢于发表自己的观点,学会分享别人的想法和结果,并重新审视自己的想法,能从交流中获益;三、教学重点:不等式的性质四、教学难点:不等式性质3的探索及运用五、教学方法:探究式教学法六、教学用具:课件七、教学时间:第一课时八、教学流程:一、复习回顾(一).等式的性质等式的基本性质1:在等式两边都加上(或减去)同一个数或整式,结果仍相等.等式的基本性质2:在等式两边都乘以或除以同一个数(除数不为0),结果仍相等.(二).解一元一次方程的基本步骤:1.去分母2.去括号3.移项4.合并同类项5.系数化为1二、提出问题引导探究(一)、用“﹥”或“﹤”填空,并总结其中的规律:(1)5>3,5+2____3+2,5-2____3-2;(2)–1<3,-1+2____3+2,-1-3____3-3;根据发现的规律填空:1、不等式的性质1:不等式的两边加(或减)同一个数(或式子),不等号的方向不变.字母表示为:如果a>b,那么a±cb±c2、不等式的性质2:不等式的两边乘(或除以)同一个正数,不等号的方向不变.字母表示为:如果a>b,c>0那么acbc,解题过程:(1)x-7>26分析:解未知数为x的不等式,就是要使不等式逐步化为x﹥a或x﹤a的形式.解:(1)为了使不等式x-7>26中不等号的一边变为x,根据不等式的性质1,不等式两边都加7,不等号的方向不变,得x-7+7﹥26+7x﹥33这个不等式的解集在数轴上的表示如图,(2)3x<2x+1为了使不等式3x<2x+1中不等号的一边变为x,根据,不等式两边都减去,不等号的方向,得0333x-2x﹤2x+1-2xx﹤1这个不等式的解集在数轴上的表示如图,注意:解不等式时也可以“移项”,即把不等式的一边的某项变号后移到另一边,而不改变不等号的方向.(3)x﹥50为了使不等式x﹥50中不等号的一边变为x,根据不等式的性质2,不等式的两边都乘不等号的方向不变,得x﹥75这个不等式的解集在数轴上的表示如图,(4)-4x﹥3为了使不等式-4x﹥3中的不等号的一边变为x,根据,不等式两边都除以,不等号的方向,得x﹤-这个不等式的解集在数轴上的表示如图,01075注意:(3)(4)的求解过程,类似于解方程两边都除以未知数的系数(未知数系数化为1),解不等式时要注意未知数系数的正负,以决定是否改变不等号的方向四、课堂练习:用不等式的性质解下列不等式,并在数轴上表示解集:(1)X+5>-1;(2)4X<3X-5;(3)X<;(4)-8X>10.(学生独立完成,集体订正)五、课堂小结:本节课你的收获是什么?※不等式的性质※不等式性质的作用将不等式化为:x﹥a或x﹤a的形式六、作业布置:作业:P1285、6题选作:习题9.1第8题七、【设计意图】设计课内、外练习,教师及时了解学生对本节知识的掌握情况,以利于对自己教学情况的掌控,并对学困生给予个别辅导,并让学生对自己所学到的知识能得到较好的利用。八、板书设计:略九、课后反思:略-430