完整版二次函数图像与性质完整归纳VIP免费

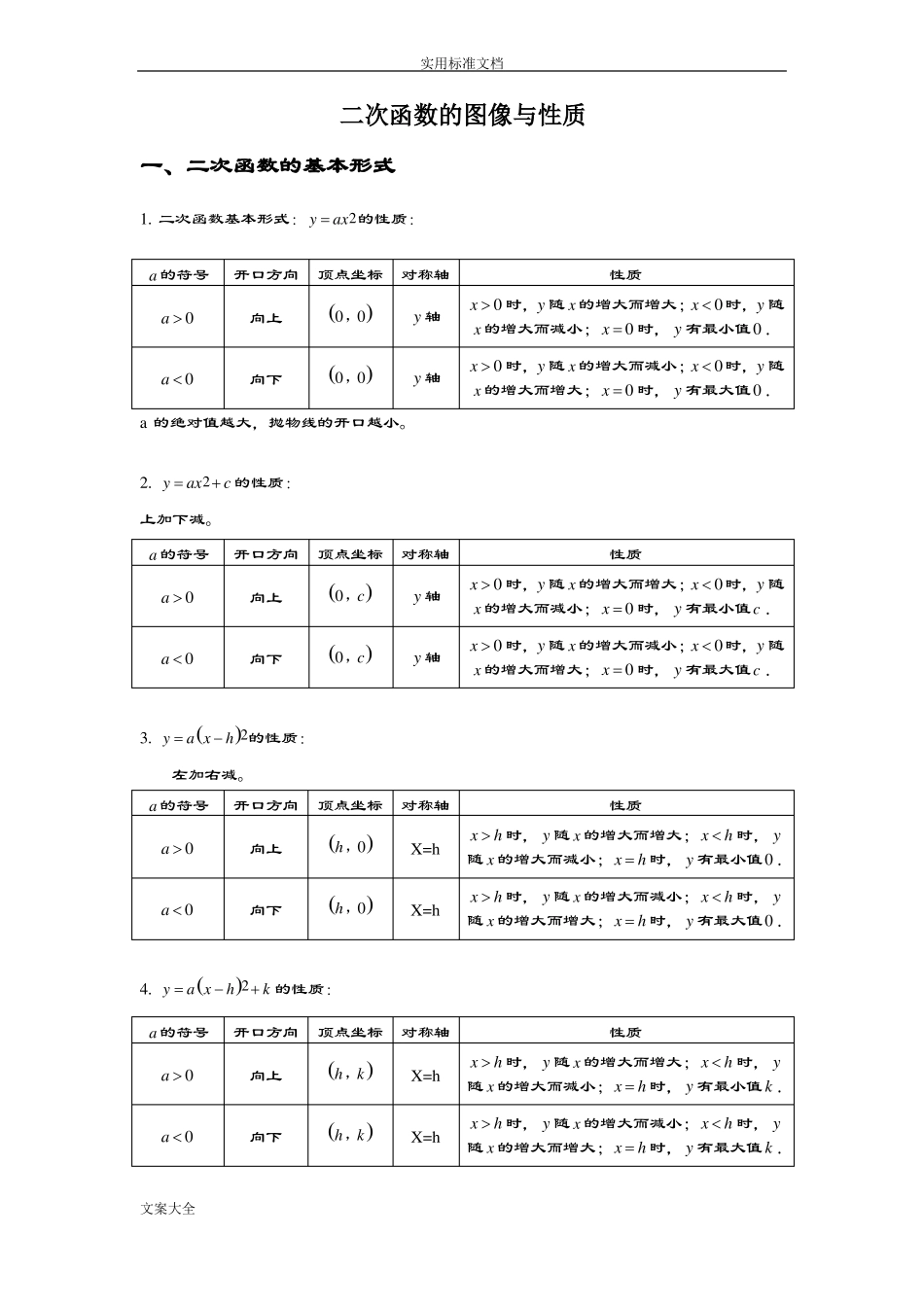
实用标准文档二次函数的图像与性质一、二次函数的基本形式1.二次函数基本形式：yax2的性质：a的符号开口方向顶点坐标对称轴向上性质a00，00，0y轴x0时，y随x的增大而增大；x0时，y随x的增大而减小；x0时，y有最小值0．x0时，y随x的增大而减小；x0时，y随x的增大而增大；x0时，y有最大值0．a0向下y轴a的绝对值越大，抛物线的开口越小。2.yax2c的性质：上加下减。a的符号开口方向顶点坐标对称轴向上性质a00，c0，cy轴x0时，y随x的增大而增大；x0时，y随x的增大而减小；x0时，y有最小值c．a0向下y轴x0时，y随x的增大而减小；x0时，y随x的增大而增大；x0时，y有最大值c．3.yaxh的性质：左加右减。a的符号2开口方向顶点坐标对称轴向上性质a0h，0X=hxh时，y随x的增大而增大；xh时，y随x的增大而减小；xh时，y有最小值0．xh时，y随x的增大而减小；xh时，y随x的增大而增大；xh时，y有最大值0．a0向下h，0X=h4.yaxhk的性质：a的符号2开口方向顶点坐标对称轴向上性质a0h，kh，kX=hxh时，y随x的增大而增大；xh时，y随x的增大而减小；xh时，y有最小值k．xh时，y随x的增大而减小；xh时，y随x的增大而增大；xh时，y有最大值k．a0向下X=h文案大全实用标准文档二、二次函数图象的平移1.平移步骤：k；方法一：⑴将抛物线解析式转化成顶点式yaxhk，确定其顶点坐标h，k处，具体平移方法如下：⑵保持抛物线yax2的形状不变，将其顶点平移到h，向上(k>0)【或向下(k<0)】平移|k|个单位2y=ax2y=ax2+k向右(h>0)【或左(h<0)】平移|k|个单位向右(h>0)【或左(h<0)】平移|k|个单位向上(k>0)【或下(k<0)】平移|k|个单位向右(h>0)【或左(h<0)】平移|k|个单位y=a(x-h)2向上(k>0)【或下(k<0)】平移|k|个单位y=a(x-h)2+k2.平移规律在原有函数的基础上“h值正右移，负左移；k值正上移，负下移”．概括成八个字“左加右减，上加下减”．方法二：⑴yaxbxc沿y轴平移:向上（下）平移m个单位，yaxbxc变成22yax2bxcm（或yax2bxcm）⑵yaxbxc沿轴平移：向左（右）平移m个单位，yaxbxc变成22ya(xm)2b(xm)c（或ya(xm)2b(xm)c）三、二次函数yaxhk与yax2bxc的比较从解析式上看，yaxhk与yax2bxc是两种不同的表达形式，后者通过配b4acb2b4acb2方可以得到前者，即yax，其中h，．k2a4a2a4a222四、二次函数yax2bxc图象的画法五点绘图法：利用配方法将二次函数yax2bxc化为顶点式ya(xh)2k，确定其开口方向、对称轴及顶点坐标，然后在对称轴两侧，左右对称地描点画图.一般我们c、c、以及0，c关于对称轴对称的点2h，选取的五点为：顶点、与y轴的交点0，0（若与x轴没有交点，则取两组关于对称轴对称的点）.0，x2，与x轴的交点x1，画草图时应抓住以下几点：开口方向，对称轴，顶点，与x轴的交点，与y轴的交点.文案大全实用标准文档五、二次函数yax2bxc的性质b4acb2b1.当a0时，抛物线开口向上，对称轴为x，顶点坐标为，．2a4a2a当xbbb时，y随x的增大而减小；当x时，y随x的增大而增大；当x2a2a2a4acb2时，y有最小值．4ab4acb2b2.当a0时，抛物线开口向下，对称轴为x，顶点坐标为，．当2a4a2axbbb时，y随x的增大而增大；当x时，y随x的增大而减小；当x时，y2a2a2a4acb2有最大值．4a六、二次函数解析式的表示方法1.一般式：yax2bxc（a，b，c为常数，a0）；2.顶点式：ya(xh)2k（a，h，k为常数，a0）；3.两根式：ya(xx1)(xx2)（a0，x1，x2是抛物线与x轴两交点的横坐标）.注意：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与x轴有交点，即b24ac0时，抛物线的解析式才可以用交点式表示．二次函数解析式的这三种形式可以互化.七、二次函数的图象与各项系数之间的关...