一次函数中特殊三角形的存在性问题VIP免费

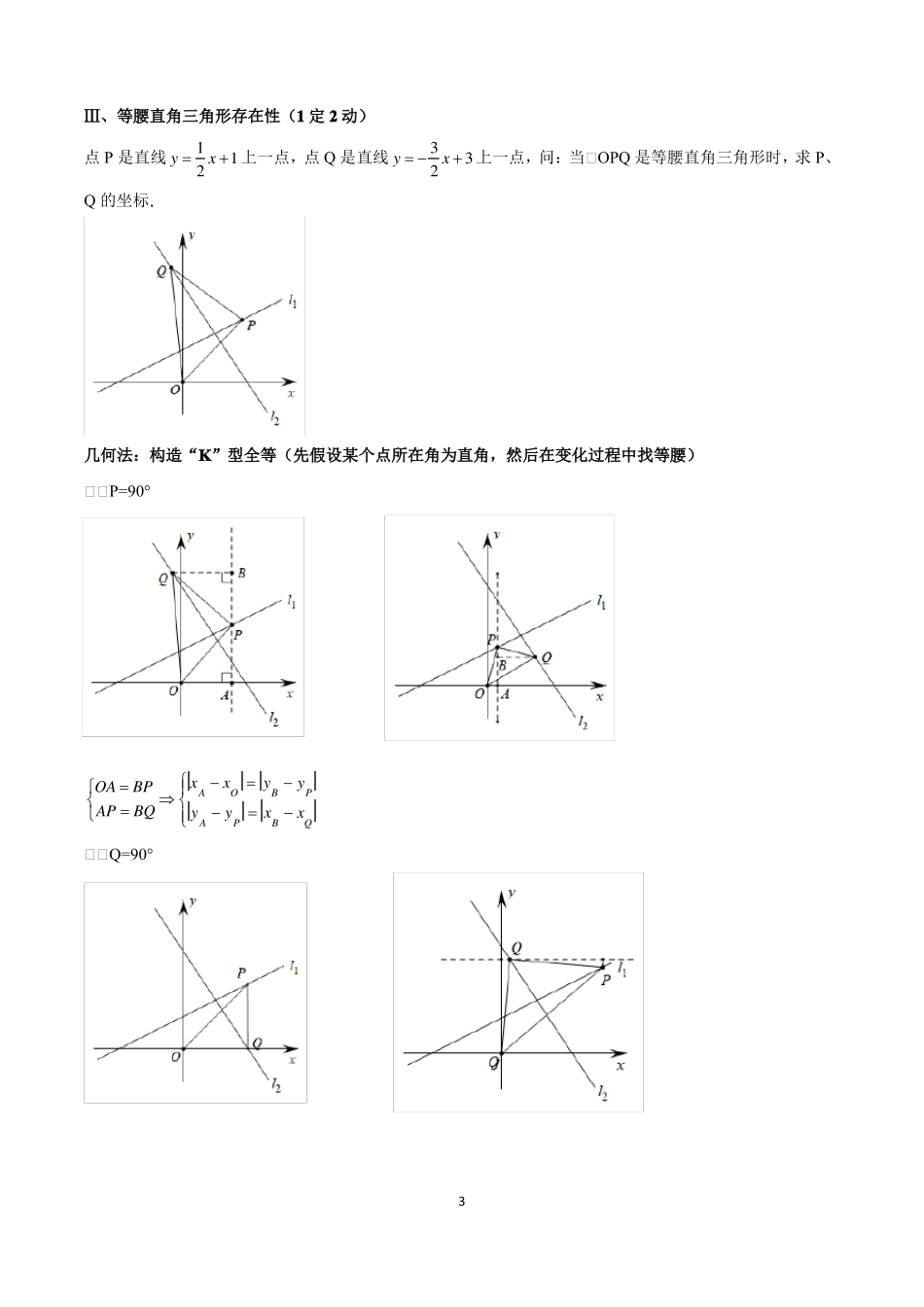
坐标系中特殊三角形的存在性问题Ⅰ、等腰三角型存在性（2定1动）直线上存在两点P、B，问：在y轴上是否存在点Q，使得△BPQ为等腰三角形，若存在，求出Q点坐标；若不存在，请说明理由．几何法：两圆一线代数法：边相等+距离公式dx1x22y1y22（1）以线段端点为圆心，线段长度为半径，画圆；B（xB，yB）、P（xP，yP）、Q（xQ，yQ）△BP=BQ时；(xBxP)2(yByP)2(xBxQ)2(yByQ)2△PB=PQ时；(xBxP)2(yByP)2(xPxQ)2(yPyQ)2△QB=QP时。(xQxB)2(yQyB)2(xPxQ)2(yPyQ)2（2）作线段的中垂线．1Ⅱ、直角三角形存在性（2定1动）直线上存在两点A、B，问：在x轴上是否存在点P，使得△ABP为等腰三角形，若存在，求出P点坐标；若不存在，请说明理由．几何法：两线一圆代数法：勾股定理+距离公式A（xA，yA）、B（xB，yB）、P（xP，yP）AB2(xAxB)2(yAyB)2AP2(xAxP)2(yAyP)2BP2(xBxP)2(yByP)2（1）过线段端点作垂线；△△A=90°AB2AP2BP2△△B=90°（2）以线段中点为圆心，线段一半为半径，画圆．AB2BP2AP2△△P=90°AP2BP2AB22Ⅲ、等腰直角三角形存在性（1定2动）点P是直线yQ的坐标．13x1上一点，点Q是直线yx3上一点，问：当△OPQ是等腰直角三角形时，求P、22几何法：构造“K”型全等（先假设某个点所在角为直角，然后在变化过程中找等腰）△△P=90°OABPxAxOyByPAPBQyyxxPBQA△△Q=90°3△△O=90°代数法：边相等+勾股定理O（xO，yO）、P（xP，yP）、Q（xQ，yQ）①∠O=90°222222OPOQ(xOxP)(yOyP)(xOxQ)(yOyQ)222222222OPOQPQ(xOxP)(yOyP)(xOxQ)(yOyQ)(xPxQ)(yPyQ)②∠P=90°222222POPQ(xOxP)(yOyP)(xPxQ)(yPyQ)222222222POPQOQ(xx)(yy)(xx)(yy)(xx)(yy)POPPQPQOQOQO③∠Q=90°222222QOQP(xQxO)(yQyO)(xQxP)(yQyP)222222222QOQPOP(xQxO)(yQyO)(xQxP)(yQyP)(xOxP)(yOyP)Ⅳ、1定2动型等腰存在性，可参考Ⅲ，先画出可能图形，再利用题中特殊关系（角度或长度关系）求解41．如图，直线l△：y＝x+2与直线l△：y＝kx+b相交于点P（1，m）（1）写出k、b满足的关系；（2）如果直线l△：y＝kx+b与两坐标轴围成一等腰直角三角形，试求直线l△的函数表达式；（3）在（2）的条件下，设直线l△与x轴相交于点A，点Q是x轴上一动点，求当△APQ是等腰三角形时的Q点的坐标．52．如图，直线ykxb与x轴、y轴分别交于点A(4，0)和点B(0，4)，点P在x轴上运动，连接PB，将△OBP沿直线BP翻折，点O的对应点记为O．（1）求k、b的值；（2）若点O恰好落在直线AB上，求△OBP的面积；（3）将线段PB绕点P顺时针旋转45°得到线段PC，直线PC与直线AB的交点为Q，在点P的运动过程中，是否存在某一位置，使得△PBQ为等腰三角形?若存在，直接写出点P的坐标；若不存在，请说明理由．63．如图1，在平面直角坐标系中，点A坐标为（﹣4，4），点B的坐标为（4，0）．（1）求直线AB的解析式；（2）点M是坐标轴上的一个点，若AB为直角边构造直角三角形△ABM，请求出满足条件的所有点M的坐标；（3）如图2，以点A为直角顶点作△CAD=90°，射线AC交x轴的负半轴与点C，射线AD交y轴的负半轴与点D，当△CAD绕点A旋转时，OC﹣OD的值是否发生变化？若不变，直接写出它的值；若变化，直接写出它的变化范围（不要解题过程）．74．在平面直角坐标系xOy中，直线l1：y＝k1x+6与x轴、y轴分别交于A、B两点，且OB＝l2：y＝k2x+b经过点C（（1）求直线l1的解析式；（2）如图1，连接CB，当CD△AB时，求点D的坐标和△BCD的面积；，1），与x轴、y轴、直线AB分别交于点E、F、D三点．OA，直线（3）如图2，当点D在直线AB上运动时，在坐标轴上是否存在点Q，使△QCD是以CD为底边的等腰直角三角形？若存在，请直接写出点Q的坐标，若不存在，请说明理由．8