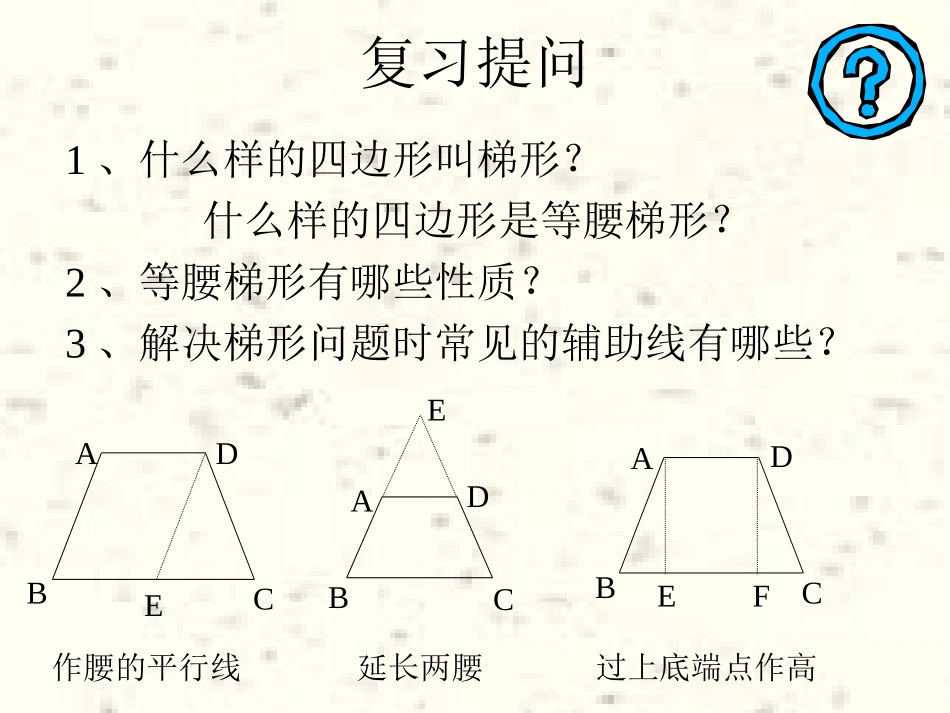
等腰梯形的判定通州市五窑初级中学任建法电话:0513-2594041邮编:226351教学目标1、熟练掌握等腰梯形的判定。2、进一步掌握解决梯形问题的基本方法,渗透转化思想,提高解决问题的能力。3、通过梯形常见辅助线添置,渗透事物相互联系和转化的观点。复习提问1、什么样的四边形叫梯形?什么样的四边形是等腰梯形?2、等腰梯形有哪些性质?3、解决梯形问题时常见的辅助线有哪些?ABDECABCDEABCDEF作腰的平行线延长两腰过上底端点作高思考:试说出等腰梯形性质定理的逆命题逆命题:在同一底上的两个角相等的梯形是等腰梯形命题:在同一底上的两个角相等的梯形是等腰梯形已知:如图,在梯形ABCD中,ADBC∥,∠B=C∠求证:AB=CDABCDE证明:过D作DEAB∥交BC于E∵DEAB∥,ADBE∥∴四边形ABED是平行四边形∴AB=DE∴∠B=1∠∴∠1=C∠∴DE=DC又ABDE∥又∠B=∠C∴AB=CD1命题:在同一底上的两个角相等的梯形是等腰梯形已知:如图,在梯形ABCD中,ADBC∥,∠B=C∠求证:AB=CDABCDE思考其他证明方法方法一:两腰向上延长相交于点E方法二:过上底两端点作高ABCDEF例1判断:⑴一组对边平行的四边形是梯形()⑵一组对边平行但不相等的四边形是梯形()⑶有一组邻角相等的梯形是等腰梯形()⑷有一组对角互补的梯形是等腰梯形()∨×∨×例2在梯形ABCD中,ADCB∥,∠A=∠D,E为AD中点。求证:EB=ECABCDE思路点拔:由∠A=D∠可得AB=CD再证△ABEDCE≌△例3求证:对角线相等的梯形是等腰梯形。已知:如图,在梯形ABCD中,ADBC∥,AC=BD求证:AB=CDABCD证明:过D作DEAC∥交BC延长线于E,则∠2=E∠E12∵ADEC∥,DEAC∥∴四边形ADEC为平行四边形∴DE=AC又∵AC=BD∴BD=DE∴∠1=E∠又∠2=E∠∴∠1=2∠又AC=DB,BC=CB∴△ABCDCB≌△∴AB=DC例4已知:如图,在△ABC中,AB=AC,BD、CE是高。求证:四边形BCDE是等腰梯形.ACBDE思路点拔:设法证DEBC∥变式一:将题中的高改为角平分线,结论是否仍成立?变式二:将题中的高改为中线,结论是否仍成立?已知:△ABC中,AB=AC,在AB上任取一点D,作DEBC∥交AC于E,试判定四边形BCED的形状并证明。ACBDE1、等腰梯形的判定方法:利用定义判定四边形为梯形,然后•证其腰相等•证其同一底上的两个角相等•证其对角线相等2、梯形中常用的辅助线.ABDECABCDEABCDEF作腰的平行线延长两腰过上底端点作高ABCDE作对角线的平行线