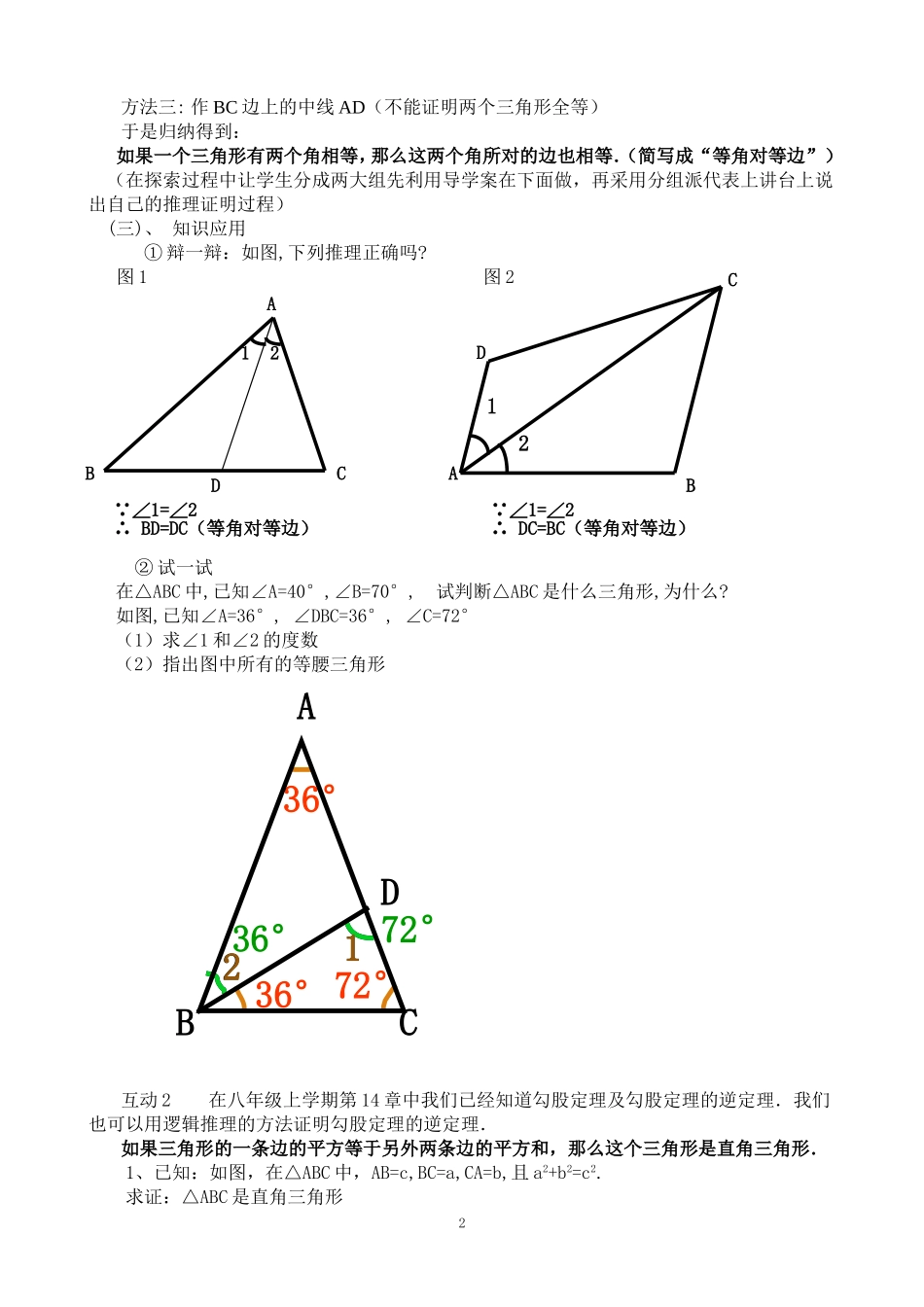
19.4逆命题与逆定理2.等腰三角形的判定泥溪镇中:于忠琼一.教学目标知识目标:理解并识记等腰三角形的判定定理,理解并识记勾股定理的逆定理;能力目标:通过分析具体问题,培养学生观察问题的能力和逻辑推理的能力;情感目标:通过亲自观察和动手操作,进一步培养学生克服困难的精神和学习兴趣,让学生树立学好数学的自信心。二.教学重难点重点:用逻辑推理的方法证明等腰三角形的判定和勾股定理的逆定理。难点:培养学生逻辑推理的能力。三.教学用具:剪刀、准备的等腰三角形及多媒体课件四.教学过程设计(一)创设情境引入1、出示一组图片,让学生观察并说出是一些什么图形?事先让学生在课下用纸自制一个等腰三角形,提出问题:(利用导学案让学生完成)什么叫等腰三角形?等腰三角形有什么性质?让同学们观察等腰三角形,同桌讨论,并思考归纳以上的两个问题,请代表回答。2、教师总结,并指出等腰三角形的这一性质的逆命题也是判定定理,是判定三角形是否是等腰三角形的一个主要方法,从而引入本节课主题--------等腰三角形的判定。(二)探究新知1、在上述情境导入的基础上提问,为什么这是判别等腰三角形的方法呢?怎么去证明呢?2、接着让同学们再次观察刚才的三角形,并给出假设,假如我们制作的三角形不是等腰三角形,而是两个角相等的三角形,我们能否证明它是等腰三角形呢?(互动1)利用全等三角形的知识解决下列问题。如图,在△ABC中,∠B=∠C。求证:AB=AC。(由学生在黑板上叙述证明过程)方法一:作∠BAC的平分线AD在△BAD和△CAD中,∠B=∠C∠1=∠2AD=AD∴△BAD≌△CAD(A.A.S)∴AB=AC(全等三角形的对应边相等)方法二:作BC边上的高AD在△BAD和△CAD中,∠B=∠C∠ADB=∠ADC=90°AD=AD∴△ABD≌△ACD(A.A.S)∴AB=AC(全等三角形的对应边相等)1ABC12D方法三:作BC边上的中线AD(不能证明两个三角形全等)于是归纳得到:如果一个三角形有两个角相等,那么这两个角所对的边也相等.(简写成“等角对等边”)(在探索过程中让学生分成两大组先利用导学案在下面做,再采用分组派代表上讲台上说出自己的推理证明过程)(三)、知识应用①辩一辩:如图,下列推理正确吗?图1图2②试一试在△ABC中,已知∠A=40°,∠B=70°,试判断△ABC是什么三角形,为什么?如图,已知∠A=36°,∠DBC=36°,∠C=72°(1)求∠1和∠2的度数(2)指出图中所有的等腰三角形互动2在八年级上学期第14章中我们已经知道勾股定理及勾股定理的逆定理.我们也可以用逻辑推理的方法证明勾股定理的逆定理.如果三角形的一条边的平方等于另外两条边的平方和,那么这个三角形是直角三角形.1、已知:如图,在△ABC中,AB=c,BC=a,CA=b,且a2+b2=c2.求证:△ABC是直角三角形36°72°1272°1236°ABC36°D2ABCD21 ∠1=∠2∴BD=DC(等角对等边)ABCD21 ∠1=∠2∴DC=BC(等角对等边)提示:构造Rt△A1B1C1,使∠C1=90°,B1C1=a,C1A1=b,然后证明△ABC≌△A1B1C1。从而可知△ABC是直角三角形。(可以先由学生在学案中做一做尝试),最后老师再板书证明过程。2、练习①下列各组数中,不能构成直角三角形的有()A.5,12,13B.6,8,10C.1,2,D.2,3,4②三角形三边长a、b、c分别是下列各组数,试判断各三角形是不是直角三角形?如果是,那么哪一个角是直角?(1)a=8,b=15,c=17;(2)a=6,b=10,c=8;(3)a=1,b=3,c=2.③若一个三角形的两边长分别是3,4,则第三边为____时,则这个三角形是直角三角形。(四)归纳总结:1.等腰三角形的判定定理是什么?直角三角形的判定定理是什么?如果一个三角形有两个角相等,那么这两个角所对应的边相等;如果三角形的一条边的平方等于另外两条边的平方和,那么这个三角形是直角三角形2.提问:①通过这一节课学习,大家有哪些体会和收获?能说说吗?②这节课我们学习了哪些数学思想方法?(同桌对讲、畅谈自己的感受和体会、学生发言,教师归纳、总结)(五)布置作业1、必做题:P91页第2题、第4题。2、选做题:两个直角三角形有两个角及一条边对应相等,这两个直角三角形全等吗?试列出各种情况,并一一加以证明。(六)板书设计等腰三角形的判定1、定义:有两边相等的三角形是...