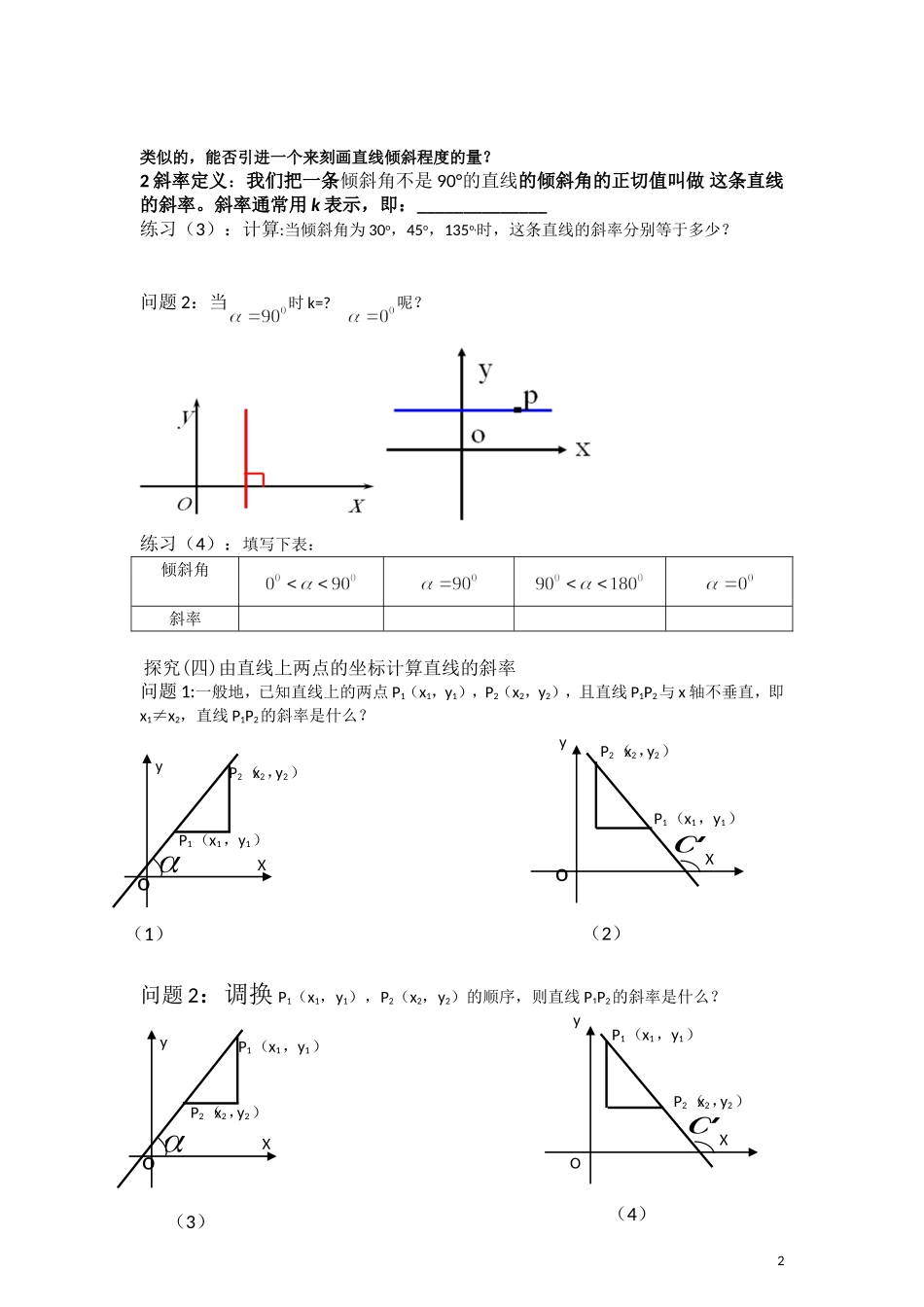
直线的倾斜角和斜率(1)长沙县实验中学刘苹学习目标:1.正确理解直线的倾斜角和斜率的概念.2.理解直线的倾斜角的唯一性.3.理解直线的斜率的存在性.4.斜率公式的推导过程,掌握过两点的直线的斜率公式.学习重点:直线的倾斜角、斜率的概念,用代数方法刻画直线斜率的过程。学习难点:直线的倾斜角与斜率之间的关系.学习过程:一、知识回顾问题1:两点能否确定一条直线?一点呢?问题2:请同学们在右下平面直角坐标系中过p任作几条直线这些直线的区别在哪里?确定直线的位置要素有哪些?二、新知探究探究(一)直线的倾斜角问题1:上述直线的方向(倾斜程度)用什么来确定?确定方向需要找一个基准,这里如何选取?请大家一起探究倾斜角的形成过程1倾斜角的定义:当直线L与x轴相交时,取___________,_________与直线L___________之间所成的角α叫做直线的倾斜角。问题2:如上所述,直角坐标平面上的每条直线是否都有一个确定的倾斜角呢?规定:当直线和x轴__________时它的倾斜角___________探究(二)倾斜角的范围:__________________练习(1):下列四图中,表示直线的倾斜角的是ABCD(2)判断对错1、所有的直线都有唯一确定的倾斜角与它对应()2、每一个倾斜角都对应于唯一的一条直线。()(3)确定直线位置的几何要素为___________________________探究(三)直线的斜率:问题1:初中学过的“坡度(比)”是什么含义?1前进2αα升高2yXyXyXyXyX类似的,能否引进一个来刻画直线倾斜程度的量?2斜率定义:我们把一条倾斜角不是90°的直线的倾斜角的正切值叫做这条直线的斜率。斜率通常用k表示,即:______________练习(3):计算:当倾斜角为30o,45o,135o,时,这条直线的斜率分别等于多少?问题2:当时k=?呢?练习(4):填写下表:倾斜角斜率探究(四)由直线上两点的坐标计算直线的斜率问题1:一般地,已知直线上的两点P1(x1,y1),P2(x2,y2),且直线P1P2与x轴不垂直,即x1≠x2,直线P1P2的斜率是什么?问题2:调换P1(x1,y1),P2(x2,y2)的顺序,则直线P1P2的斜率是什么?2(4)P2(x2,y2)P1(x1,y1)yOX(2)P2(x2,y2)P1(x1,y1)yoX(3)P2(x2,y2)P1(x1,y1)oyX(1)P2(x2,y2)P1(x1,y1)oyX问题3:当直线平行于x轴,或与x轴重合时,上述公式还适用吗?为什么?问题4:当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?3斜率公式:练习(5)判断正误:②任一条直线都有倾斜角,也都有斜率,())③因为平行于轴的直线的斜率不存在,所以平行于轴的直线的倾斜角不存在,()④两直线的斜率相等,它们的倾斜角相等,()三、典例精析:例1已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断它们的倾斜角是钝角还是锐角.四、课堂小结:本节课我们学习了那些数学知识、数学方法?用到了那些数学思想?3yyOXoxyoxy