同角三角函数的基本关系2VIP免费

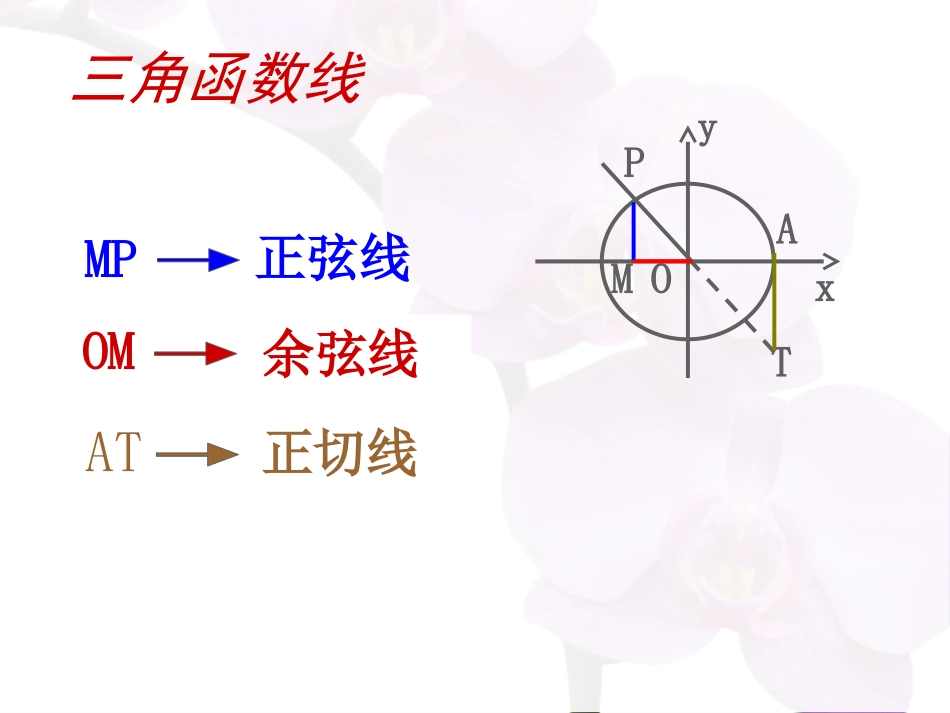
同角三角函数的基本关系永康一中：单一明ryasinrxacostan(0)yaxx温故而知新：1、设为任意角，它的终边上一点P的坐标为P(x,y)，则2、三角函数值在各象限的符号：22rxyyxosinyxocosyxotan+-+---++-++-三角函数线POxyMATMP正弦线OM余弦线AT正切线归纳探索sincostan123233222213212312323322sincossincos22sincos1sintancos111133133363465探究：22sincos1sintancos对于任意角还成立吗？自己尝试证明一下cosxrsinyαrtanyx22sincos1sintancosPOxyMAT1.定义法：2.数形结合MP2+OM2=OP2=1sin2α+cos2α=1yxP,22yxr令同一个角的正弦、余弦的平方和等于1，商等于这个角的正切.22sincos1sintancos平方关系：商数关系：同角关系(Z)2kk文字表述：3sin,cos,tan.5例1已知求的值43tan,54-cos:为第三象限时43tan,54cos为第四象限时：为第三或第四象限角cos1cossin22解题步骤：（1）确定象限（2）确定符号（3）求值例题讲解1sin.cosxxcosx例3、求证：1-sinx证明：因为（1-sinx）(1+sinx)2cosxx2=1-sin=cosxcosx,1sin.cosxx且1-sinx0,cosx0，所以cosx1-sinx分组讨论1sin.cosxxcosx例3、求证：1-sinx证明：由cosx0,知sinx-1,所以1+sinx0,于是(1sin)(1sin)xxcosx(1+sinx)左边=xx22cosx(1+sinx)1-sincosx(1+sinx)cos1+sinx==右边.cosx所以原式成立。证明：由cosx0,知sinx1,所以1-sinx0,于是(1+sinx)(1-sinx)右边=cosx(1-sinx)1sin.cosxxcosx例3、求证：1-sinxx221-sincosx(1-sinx)cosxcosx(1-sinx)cosx==左边.1-sinx所以原式成立。1sin.cosxxcosx例3、求证：1-sinx证明：因为左边－右边cosx1+sinx＝－1-sinxcosx2cosx-(1-sinx)(1+sinx)＝cosx(1-sinx)0,x22cosx-cos=cosx(1-sinx)所以原式成立。小结：本节课你收获了什么？22sincos1sintancos应用