相似三角形的性质VIP免费

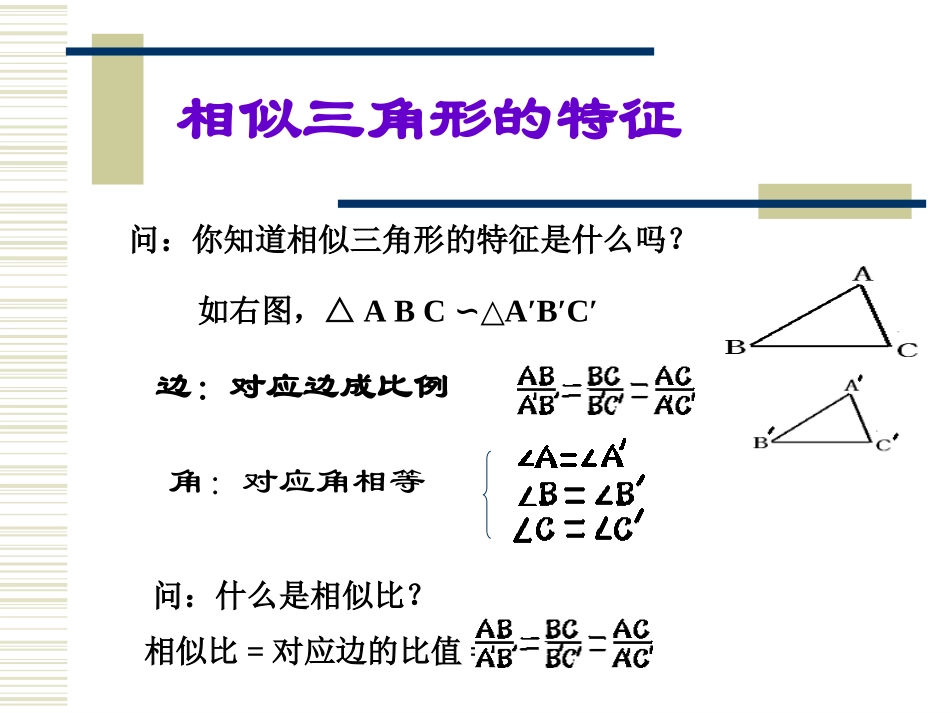
相似三角形的性质相似三角形的性质授课:杨艳红第三章图形的相似相似三角形的识别问：相似三角形的识别方法有哪些？证二组对应角相等证三组对应边成比例证二组对应边成比例，且夹角相等相似三角形的特征问：你知道相似三角形的特征是什么吗？角：对应角相等边：对应边成比例问：什么是相似比？相似比=对应边的比值=如右图，△ABCA′B′C′∽△思考相似三角形可看作是一个三角形放大（或缩小）所得到的，那么三角形中重要的三线＂高、中线、角平分线＂是否会随三角形的放大（或缩小）而一起放大（或缩小）．即如果相似三角形的相似比为k，那么相似三角形的对应高的比、对应中线的比、对应角平分线的比和k之间有何关系呢？相似三角形对应边上的高有什么关系呢？归纳：相似三角形对应边上的高之比等于相似比。A′B′C′D′△ADCA′D′C′∽△则:(1)利用方格把三角形扩大2倍，得△A′B′C′，并作出B′C′边上的高A′D′。△ABC与△A′B′C′的相似比为多少？AD与A′D′有什么关系？右图△ABC，AD为BC边上的高。DABC(2)如右图两个相似三角形相似比为k，则对应边上的高有什么关系呢？__________说说你判断的理由是什么？___________归纳：相似三角形对应边上的中线比等于相似比。相似三角形对应边上的中线有什么关系呢？如右图△ABC，AE为BC边上的中线。则:(1)把三角形扩大2倍后得△A′B′C′，A′E′为B′C′边上的中线。△ABC与△A′B′C′的相似比为多少？AE与A′E′比是多少？ABCEA′B′C′E′△AECA′E′C′∽△(2)如右图两个相似三角形相似比为k，则对应边上的中线的比是多少呢？说说你判断的理由是什么？___________相似三角形对应角的角平分线有什么关系呢？归纳：相似三角形对应角的角平分线之比等于相似比。(2)如右图两个相似三角形相似比为k，则对应角的角平分线比是多少？说说你判断的理由是什么？___________△AFCA′F′C′∽△如右图△ABC，AF为∠A的角平分线。则:(1)把三角形扩大2倍后得△A′B′C′，A′F′为∠A′的角平分线，△ABC与△A′B′C′的相似比为多少？AF与A′F′比是多少？ABCFA′B′C′F′判断下列结论是否正确（1）相似三角形的中线比等于相似比。（2）两个相似三角形的高的比等于它们边长的比。填一填1、两个相似三角形对应边比为3:5，那么相似比为，对应边上的高之比为，对应边上的中线比为，对应角的角平分线比为。2、两个相似三角形对应角的角平分线比为1:4，可直接得到对应边上的高之比为，对应边上的中线比为。3、△ABC的三边分别为3、4、5，△A′B′C′的三边长分别为12、16、x,则x=。3:53:53:53:51:41:420课堂练习4、已知△ABC∽△A′B′C′的相似比为2：3，则它们对应中线的比为；5、已知两个相似三角形对应高的比是4：1，则它们的对应角平分线的比是；6、已知△ABC∽△DEF且BC=3，EF=6，DE边上的中线为10，那么AB边上的中线为。7、已知△ABC∽△A′B′C′，AD和A′D′分别是△ABC∽△A′B′C′的角平分线，且AD：A′D′=3：2，AB=9，则A′B′=已知△ABC和△A1B1C1中，AD和BE是△ABC的高，A1D1和B1E1是△A1B1C1的高，且∠C＝∠C1，求证：1111BAABDAAD1111EBBEDAAD提高训练小结相似三角形的性质对应角相等、对应边成比例；对应高之比等于相似比；对应中线之比等于相似比；对应角平分线之比等于相似比。（你学到了什么呢？）