一元二次方程根与系数的关系VIP免费

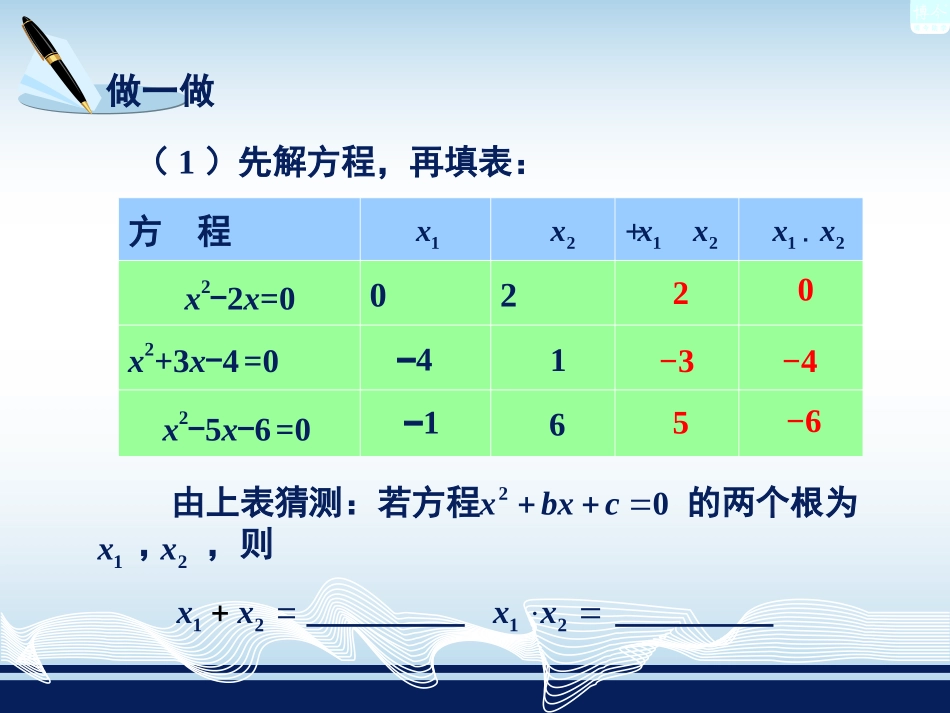
一元二次方程根与系数的关系本节内容2.4我们已经知道，一元二次方程的根的值由方程的系数a，b，c来决定，除此之外，根与系数之间还有什么关系呢？ax2+bx+c=0(a≠0)做一做方程+02x2+3x-4=0x2-2x=0x2-5x-6=0x1x2x1·（1）先解方程，再填表：x2x2x1由上表猜测：若方程的两个根为，，则20xbxcx2x112xx12xx−16−4120−3−45−6(x-)256xx(x-)（2）方程的两个根为，，根据2.2节例8下面的一段话，得x2x12560xx23动脑筋对于方程ax2+bx+c=0(a≠0)，当Δ≥0时，该方程的根与它的系数之间有什么关系呢？当Δ≥0时，设ax2+bx+c=0（a≠0）的两个根为，，则x2x121221212==，axbxcaxxxxaxxxxxx22，bcaxbxcaxxaa又221212.bcxxxxxxxxaa于是12.cxxa根据七年级上册教科书2.5节关于两个多项式相等的规定，得12,bxxa结论1212bcxx,xxaa即这个关系通常被称为韦达定理.这表明，当Δ≥0时，一元二次方程的根与系数之间具有如下关系：两根的和等于一次项系数与二次项系数的比的相反数，两根的积等于常数项与二次项系数的比.举例例1根据一元二次方程根与系数的关系，求下列方程的两根，的和与积:（1）2x2-3x+1=0（2）x2-3x+2=10（3）7x2-5=x+8x2x1举例例1根据一元二次方程根与系数的关系，求下列方程的两根，的和与积:（1）2x2-3x+1=01212331.222xx,xx解（2）x2-3x+2=101212338.xx,xx整理，得x2-3x-8=0，所以解（3）7x2-5=x+8解1212111313.7777xx,xx整理，得7x2-x-13=0，所以举例例2已知关于x的方程的一个根为-3，求它的另一个根及q的值.230xxq++设的另一个根为则解230xxq++2x,（-3）+=-3.x2解得.20x因此，方程的另一个根是0，q的值为0.由根与系数之间的关系得300q.（）还可用其他方法求出q的值吗？练习1.根据一元二次方程根与系数的关系，求下列方程的两根的和与积：（1）x2-6x+1=0；（2）2x2-x=6.（1）x2-6x+1=0（2）2x2-x=61212116=3.222xx,xx解1212(6)61.xx,xx解原方程可化为2x2-x-6=0,2.已知方程的一个根为1，求它的另一个根及m的值：23190xxm∴19161.33a19191,33a解设此方程的另一个根为a，则有1,3ma又∴163316.3ma结束