湘教版：全等三角形判定定理㈠VIP免费

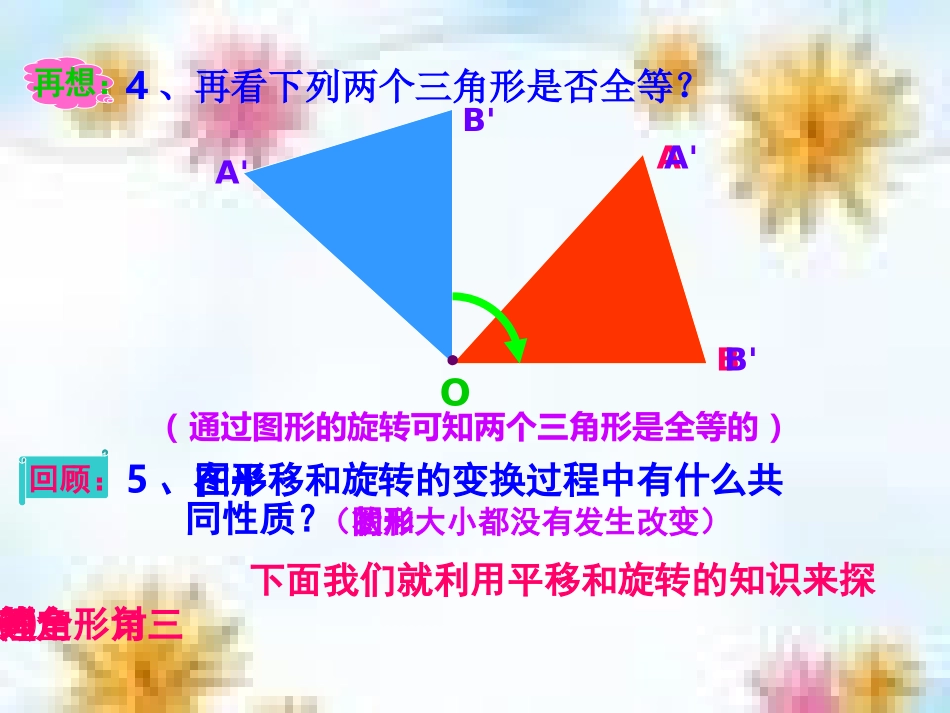
全等三角形判定定理㈠（SAS）边角边定理湖南沅陵大合坪乡九校教师曹新建2010年12月10日制湘教版一、温故知新：1、什么样的两个三角形叫全等三角形？答：能够相互重合的两个三角形叫全等三角形。2、全等三角形有哪些性质？答：全等三角形的对应边相等、对应角相等。ACBB′A′C′（通过图形的平移可知两个三角形是全等的）回顾：3、下列两个三角形是否全等？想想：4、再看下列两个三角形是否全等？ABA'B'O．A'B'（通过图形的旋转可知两个三角形是全等的）再想：回顾：（图形的形状和大小都没有发生改变）5、图形在平移和旋转的变换过程中有什么共同性质？下面我们就利用平移和旋转的知识来探讨三角形全等的判定方法㈠：边角边定理！二、讲授新课：如果在△ABC和△A'B'C'中，AB=A'B'，∠B=∠B'，BC=B'C'，那么△ABC和△A'B'C'全等吗？问题：探究㈠：⑴、如果△ABC和△A'B'C'的位置关系如图①所示，则两个三⑴、角形全等吗？ABCC'(B')A'．A'C'即将△A'B'C'绕顶点B旋转，使B'C'与BC重合。思考：能否通过图形旋转试试？旋转演示：发现：通过旋转演示我们发现：当B'C'与BC重合时，又 ∠B'=∠B，A'B'=AB，∴A'B'与AB也重合，从而A'C'与AC也重合了，于是△A'B'C'和△ABC就完全重合了，因此得出△ABC≌△A'B'C'。（图①）⑵、如果△ABC和△A'B'C'的位置关系如图②所示，则两个三角形全等吗？探究㈡：C'A'B'B'A'C'BCA．（图②）能否通过图形的平移和旋转试试？思考：即先将△A'B'C'平移，使顶点B'与△ABC的顶点B重合后，再绕点B旋转，使B'C'与BC重合。变换演示：发现：通过变换演示我们发现：当B'C'与BC重合时，又 ∠B'=∠B，A'B'=AB，∴A'B'与AB也重合，从而A'C'与AC也重合了，于是△A'B'C'和△ABC就完全重合了，因此也得出△ABC≌△A'B'C'。发散：本⑵小题的变换还有无其它方式？请同学们再看变换演示！变换演示：当然变换的方式还有，这里就不再讲了，请同学们课后自行想想。探究㈢：⑶、如果△ABC和△A'B'C'的位置关系如图③所示，则两个三角形全等吗？思考：变换演示：（图③）A'B'C'A'B'C'ABCA'B'C'能否通过图形轴对称和平移试试？即先把△A'B'C'以直线m为轴作轴反射，再把轴反射所得的图形平移与△ABC重合。当然也可把△A'B'C'以边B'C'为轴作轴反射后，再平移。m发现：通过变换演示我们发现：△A'B'C'和△ABC已完全重合了，从而也得出△ABC≌△A'B'C'。归纳：通过对上面有相同已知条件，只是图形的位置不同的三个小题的探讨与分析，我们可得出判定三角形全等的一种方法：边角边定理有两边和它们的夹角对应相等的两个三角形全等（可简写成“边角边”或“SAS”）。三、教学实例：例1：如右图，AB和CD相交于点O，且AO=BO，CO=DO，求证：△ACO≌△BDO。AoCBD分析：在△ACO和△BDO中：AO=BO（已知）CO=DO（已知）∠AOC=∠BOD（从图上可知：它们是对顶角，且我们又知道对顶角相等）可见：该题中的两个三角形满足边角边定理所叙述的内容，即有两边和它们的夹角对应相等，因此这两个三角形全等。证明：在△ACO和△BDO中：AO=BO（已知）∠AOC=∠BOD（对顶角相等）CO=DO（已知） ∴△ACO≌△BDO（SAS）注意：所以，△ACO与△BDO全等。由于同学们学证明的时间不够长，所以做题时应特别注意证明的每一步都要有根据，这些根据可以是题中的已知条件（特别要会从题中的图形上找出隐含的已知条件，即要会看图），也可是我们学过的公理、定理和定义。另外证明三角形全等时还要注意对应顶点应书写在对应的位置上！例2：A'B'ABO分析：如右下图，正在修建的某高速公路要通过一座大山，现要从这座山中挖一条隧道，为了预算这条隧道的造价，必须知道隧道的长度，即这座山A、B两处的距离，你能想出一个办法，测出AB的长度吗？．．解：如右图，确定点O，使点O可以到达A与B两点。．连结AO并延长AO至A'，使OA'=OA；连结BO并延长BO至B'，使OB'=OB；再连结A'B'。在△AOB和△A'OB'中：要想直接测出AB的长度是不可能的，怎么办？我们应在大山外的开阔地选择一合适的地点O，使得从点O可以到达A、B两处，并测出AO与BO的长度。连结AO并延长AO至A'，使OA'=OA；连结BO并延长BO至B'，使OB'=OB，再连结A'B'，然后只需证B，...