相交线与平行线VIP免费

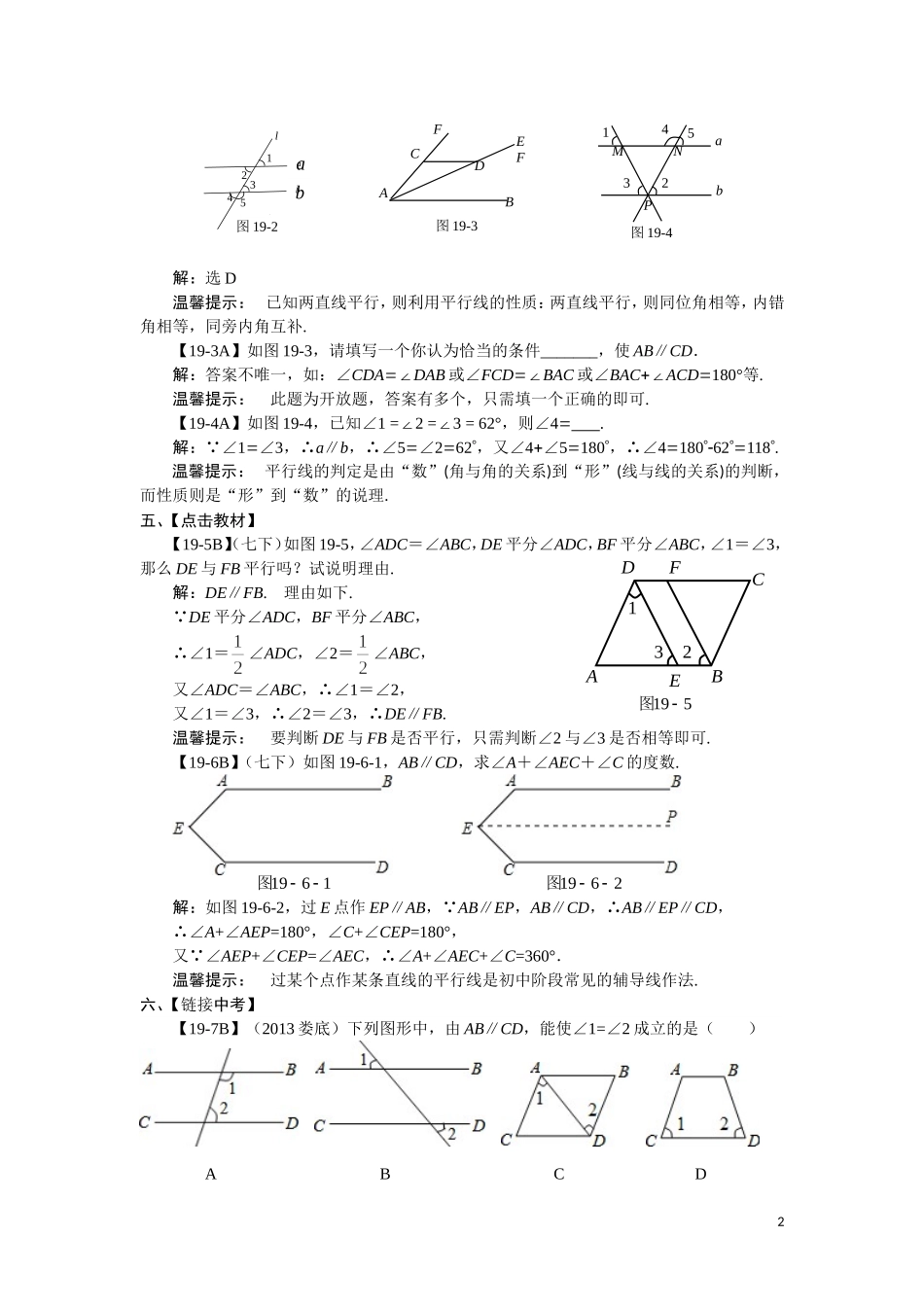
OEDCBA图19-1第19课时相交线与平行线一、【教学目标】1．了解对顶角的概念；2．掌握对顶角相等；3．了解垂线、垂线段的概念、画法及性质，了解点到直线的距离；4．掌握“过一点有且只有一条直线与已知直线垂直”；5．理解线段垂直平分线及性质；6．了解同位角、内错角、同旁内角；7．理解平行线的概念；8．掌握“过直线外一点有且只有一条直线与已知直线平行”；9．掌握平行线的性质和判定；10．体验平行线间的距离；11．掌握平行线的画法二、【重点难点】1．平行线的性质和判定；2．线段垂直平分线的性质；三、【主要考点】（一）、相交线1．对顶角：对顶角相等.2．垂线：⑴过一点有且只有一条直线与已知直线垂直；⑵垂线段最短.3．点到直线的距离：直线外一点到这条直线的垂线段的长度.（二）、平行线1．平行公理：（1）经过直线外一点，有且只有一条直线与这条直线平行.（2）如果a∥b，a∥c，那么b∥c.2．性质与判定（1）两直线平行同位角相等；（2）两直线平行内错角相等；（3）两直线平行同旁内角互补.说明：由平行到角是性质，由角到平行是判定.四、【经典题型】【19-1A】如图19-1，直线AB与直线CD相交于点O，E是∠AOD内一点，已知OE⊥AB，∠BOD=，则∠COE的度数是()A.125°B.135°C.145°D.155°解： ∠AOC与∠BOD是对顶角，∴∠AOC∠BOD45， OE⊥AB，∴∠AOE90，∴∠COE∠AOC∠AOE4590135.选B.【19-2A】如图19-2，已知a∥b，l分别与a、b相交，下列结论中错误的是（）A．∠1=∠3B.∠2=∠3C.∠1=∠4D.∠2=∠51解：选D温馨提示：已知两直线平行，则利用平行线的性质：两直线平行，则同位角相等，内错角相等，同旁内角互补.【19-3A】如图19-3，请填写一个你认为恰当的条件_______，使AB∥CD．解：答案不唯一，如：∠CDA∠DAB或∠FCD∠BAC或∠BAC∠ACD180°等.温馨提示：此题为开放题，答案有多个，只需填一个正确的即可.【19-4A】如图19-4，已知∠1=∠2=∠3=62°，则∠4.解： ∠1∠3，∴a∥b，∴∠5∠262，又∠4∠5180，∴∠418062118.温馨提示：平行线的判定是由“数”(角与角的关系)到“形”(线与线的关系)的判断，而性质则是“形”到“数”的说理.五、【点击教材】【19-5B】（七下）如图19-5，∠ADC＝∠ABC，DE平分∠ADC，BF平分∠ABC，∠1＝∠3，那么DE与FB平行吗？试说明理由.解：DE∥FB.理由如下. DE平分∠ADC，BF平分∠ABC，∴∠1＝∠ADC，∠2＝∠ABC，又∠ADC＝∠ABC，∴∠1＝∠2，又∠1＝∠3，∴∠2＝∠3，∴DE∥FB.温馨提示：要判断DE与FB是否平行，只需判断∠2与∠3是否相等即可.【19-6B】（七下）如图19-6-1，AB∥CD，求∠A＋∠AEC＋∠C的度数.解：如图19-6-2，过E点作EP∥AB， AB∥EP，AB∥CD，∴AB∥EP∥CD，∴∠A+∠AEP=180°，∠C+∠CEP=180°，又 ∠AEP+∠CEP=∠AEC，∴∠A+∠AEC+∠C=360°．温馨提示：过某个点作某条直线的平行线是初中阶段常见的辅导线作法.六、【链接中考】【19-7B】（2013娄底）下列图形中，由AB∥CD，能使∠1=∠2成立的是（）ABCD图19-2第8题54321lbababFCABDEF图19-3MNPab12345图19-41961图1962图2195图ABCDFE123解：A、由AB∥CD可得∠1+∠2=180°，故本选项错误；B、如图19-7， AB∥CD，∴∠1=∠3，又 ∠2=∠3（对顶角相等），∴∠1=∠2，故本选项正确；C、由AC∥BD得到∠1=∠2，由AB∥CD不能得到∠1=∠2，故本选项错误；D、梯形ABDC是等腰梯形才可以有∠1=∠2，故本选项错误．故选B．温馨提示：平行线的常用性质有：①两直线平行，同位角相等；②两直线平行，内错角相等；③两直线平行，同旁内角互补；④在平面内，如果一条直线垂直于两平行线中的一条，那么这条直线必垂直于另一条.【19-8C】（2015黔南州）如图19-8，下列说法错误的是（）A．若a∥b，b∥c，则a∥cB．若∠1=∠2，则a∥cC．若∠3=∠2，则b∥cD．若∠3+∠5=180°，则a∥c解：A、若a∥b，b∥c，则a∥c，利用了平行公理，正确；B、若∠1=∠2，则a∥c，利用了内错角相等，两直线平行，正确；C、∠3=∠2，不能判断b∥c，错误；D、若∠3+∠5=180°，则a∥c，利用同旁内角互补，两直...