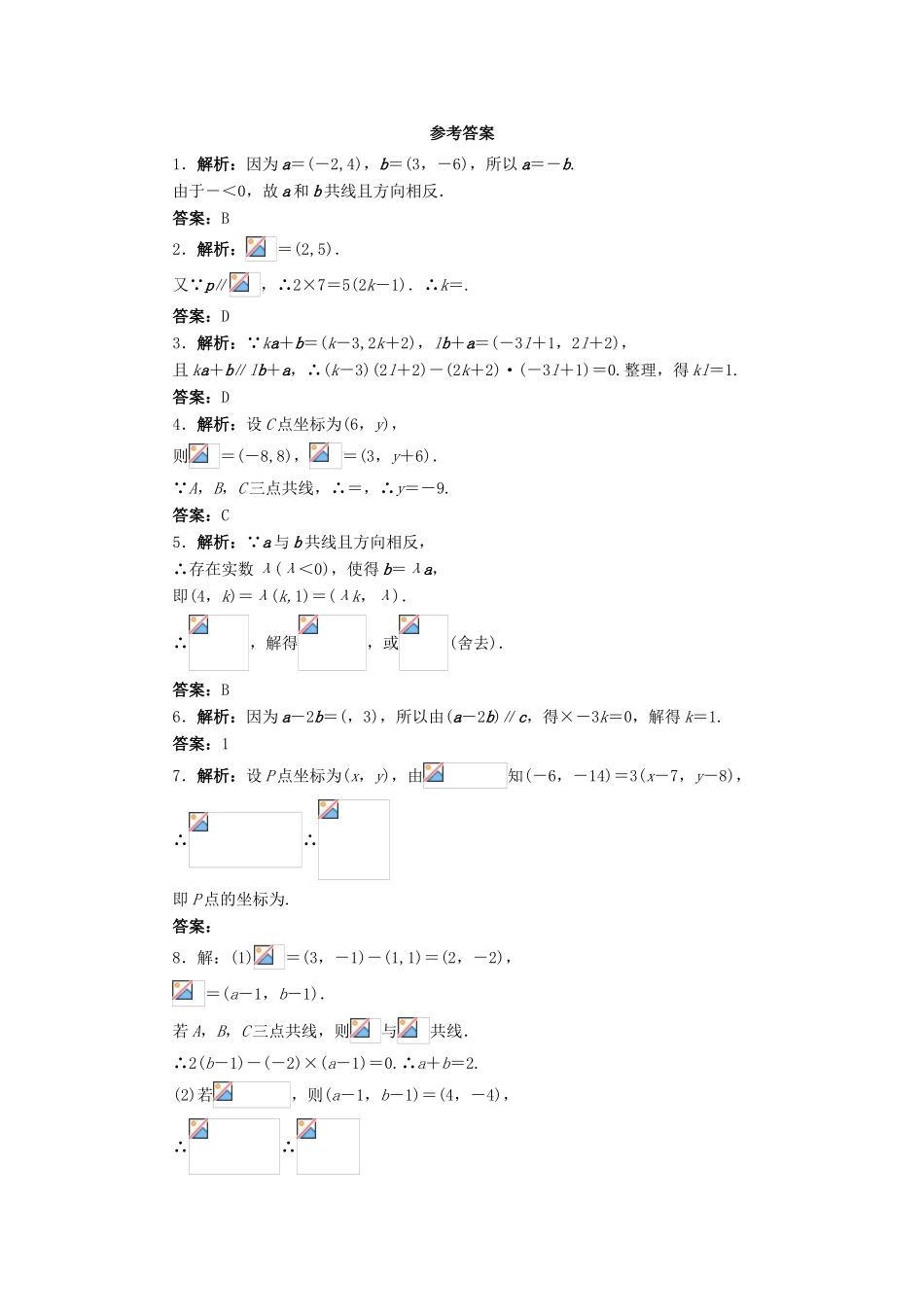
2.4平面向量的坐标自我小测1.已知向量a=(-2,4),b=(3,-6),则a和b的关系是()A.共线且方向相同B.共线且方向相反C.是相反向量D.不共线2.已知A(2,-2),B(4,3),向量p的坐标为(2k-1,7),且p∥,则k的值为()A.-B.C.-D.3.已知向量a=(1,2),b=(-3,2),且向量ka+b与lb+a平行,则实数k,l满足的关系式为()A.kl=-1B.k+l=0C.l-k=0D.kl=14.已知A,B,C三点在一条直线上,且A(3,-6),B(-5,2),若C点的横坐标为6,则C点的纵坐标为()A.-13B.9C.-9D.135.如果向量a=(k,1),b=(4,k)共线且方向相反,则k等于()A.±2B.-2C.2D.06.已知向量a=(,1),b=(0,-1),c=(k,),若a-2b与c共线,则k=__________.7.已知两点M(7,8),N(1,-6),P点是线段MN的靠近点M的三等分点,则P点的坐标为__________.8.已知A(1,1),B(3,-1),C(a,b).(1)若A,B,C三点共线,求a,b的关系式;(2)若,求点C的坐标.9.已知向量a=(1,2),b=(x,6),u=a+2b,v=2a-b,(1)若u∥v,求实数x的值;(2)若a,v不共线,求实数x的值.参考答案1.解析:因为a=(-2,4),b=(3,-6),所以a=-b.由于-<0,故a和b共线且方向相反.答案:B2.解析:=(2,5).又∵p∥,∴2×7=5(2k-1).∴k=.答案:D3.解析:∵ka+b=(k-3,2k+2),lb+a=(-3l+1,2l+2),且ka+b∥lb+a,∴(k-3)(2l+2)-(2k+2)·(-3l+1)=0.整理,得kl=1.答案:D4.解析:设C点坐标为(6,y),则=(-8,8),=(3,y+6).∵A,B,C三点共线,∴=,∴y=-9.答案:C5.解析:∵a与b共线且方向相反,∴存在实数λ(λ<0),使得b=λa,即(4,k)=λ(k,1)=(λk,λ).∴,解得,或(舍去).答案:B6.解析:因为a-2b=(,3),所以由(a-2b)∥c,得×-3k=0,解得k=1.答案:17.解析:设P点坐标为(x,y),由知(-6,-14)=3(x-7,y-8),∴∴即P点的坐标为.答案:8.解:(1)=(3,-1)-(1,1)=(2,-2),=(a-1,b-1).若A,B,C三点共线,则与共线.∴2(b-1)-(-2)×(a-1)=0.∴a+b=2.(2)若,则(a-1,b-1)=(4,-4),∴∴∴点C的坐标为(5,-3).9.解:(1)因为a=(1,2),b=(x,6),u=a+2b,v=2a-b,所以u=(1,2)+2(x,6)=(2x+1,14),v=2(1,2)-(x,6)=(2-x,-2).又因为u∥v,所以-2(2x+1)-14(2-x)=0,即10x=30,解得x=3.(2)若a,v共线,则2(2-x)=-2,解得x=3,所以要使a,v不共线,则{x|x∈R,且x≠3}.