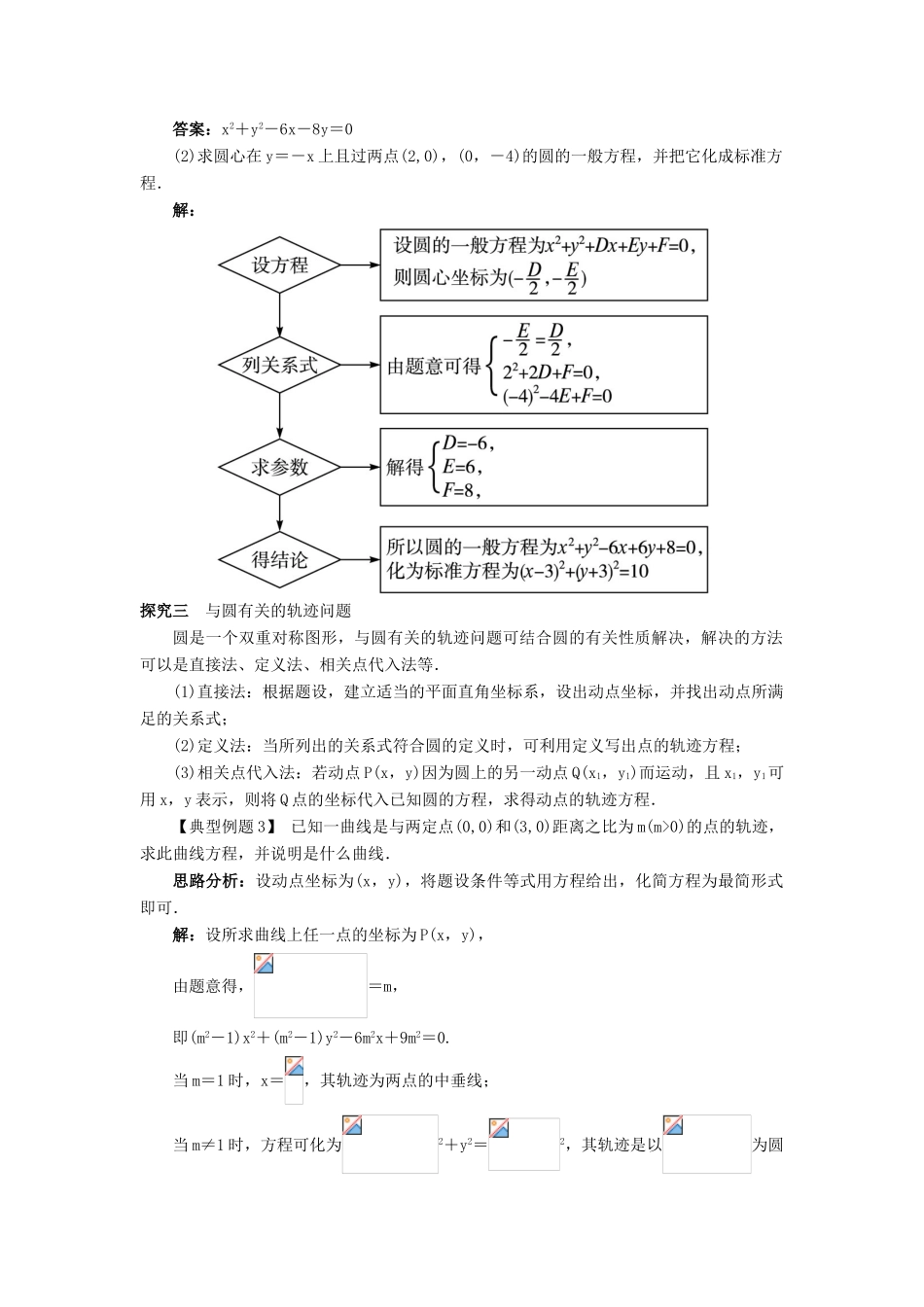
2.3.2圆的一般方程课堂探究探究一二元二次方程表示圆的条件方程x2+y2+Dx+Ey+F=0表示圆的两种判断方法:(1)(配方法)对形如x2+y2+Dx+Ey+F=0的二元二次方程可以通过配方变形成“标准”形式后,观察是否表示圆;(2)(运用圆的一般方程的判断方法求解)即通过判断D2+E2-4F是否为正,确定它是否表示圆.【典型例题1】若关于x,y的方程x2+mxy+y2+2x-y+n=0表示的曲线是圆,则m+n的取值范围是()A.B.C.D.解析:因为x2+mxy+y2+2x-y+n=0表示圆,所以解得n<,所以m+n<.答案:A探究二用待定系数法求圆的方程1.用待定系数法求圆的方程的大致步骤如下:2.对圆的一般方程和标准方程的选择:(1)如果由已知条件容易求得圆心坐标、半径或需利用圆心的坐标或半径来列方程的问题,一般采用圆的标准方程,再用待定系数法求出a,b,r.(2)如果已知条件和圆心或半径都无直接关系,一般采用圆的一般方程,再利用待定系数法求出常数D,E,F.【典型例题2】(1)已知A(-1,1),B(6,0),C(-1,7),则△ABC的外接圆的方程是__________.解析:设圆的方程是x2+y2+Dx+Ey+F=0,将A,B,C三点的坐标代入方程,解方程组得D=-6,E=-8,F=0,从而圆的方程为x2+y2-6x-8y=0.答案:x2+y2-6x-8y=0(2)求圆心在y=-x上且过两点(2,0),(0,-4)的圆的一般方程,并把它化成标准方程.解:探究三与圆有关的轨迹问题圆是一个双重对称图形,与圆有关的轨迹问题可结合圆的有关性质解决,解决的方法可以是直接法、定义法、相关点代入法等.(1)直接法:根据题设,建立适当的平面直角坐标系,设出动点坐标,并找出动点所满足的关系式;(2)定义法:当所列出的关系式符合圆的定义时,可利用定义写出点的轨迹方程;(3)相关点代入法:若动点P(x,y)因为圆上的另一动点Q(x1,y1)而运动,且x1,y1可用x,y表示,则将Q点的坐标代入已知圆的方程,求得动点的轨迹方程.【典型例题3】已知一曲线是与两定点(0,0)和(3,0)距离之比为m(m>0)的点的轨迹,求此曲线方程,并说明是什么曲线.思路分析:设动点坐标为(x,y),将题设条件等式用方程给出,化简方程为最简形式即可.解:设所求曲线上任一点的坐标为P(x,y),由题意得,=m,即(m2-1)x2+(m2-1)y2-6m2x+9m2=0.当m=1时,x=,其轨迹为两点的中垂线;当m≠1时,方程可化为2+y2=2,其轨迹是以为圆心,以为半径的圆.点评求轨迹方程与轨迹是不同的,求轨迹方程时只需要求出方程,求轨迹时,不仅要求出轨迹方程,还要指出方程表示的图形,如果方程中含有参数要分类讨论,如有不符合条件的点要舍去.【典型例题4】已知点P在圆C:x2+y2-8x-6y+21=0上运动,求线段OP的中点M的轨迹方程.解法一:设点M(x,y),点P(x0,y0),则所以因为点P(x0,y0)在圆C:x2+y2-8x-6y+21=0上,所以x20+y20-8x0-6y0+21=0.所以(2x)2+(2y)2-8·(2x)-6·(2y)+21=0.即点M的轨迹方程为x2+y2-4x-3y+=0.解法二:设点M的坐标为(x,y),连接OC,PC,取线段OC的中点A,连接MA.圆C的方程可化为(x-4)2+(y-3)2=4,圆心C(4,3),|CP|=2,则点A的坐标为.如图所示,在△OCP中,M,A分别是OP,OC的中点,则|MA|=|CP|,即|MA|=1.又当O,C,P三点共线时,|MA|=1.所以点M的轨迹是以A为圆心,1为半径的圆.所以点M的轨迹方程为(x-2)2+2=1.探究四求圆关于点(线)对称的圆1.求圆C:(x-a)2+(y-b)2=r2关于点P(x0,y0)对称的圆的方程,首先要找出圆心C(a,b)关于点P(x0,y0)的对称点,得到对称圆的圆心,半径不变,即得所求圆的方程.2.求圆关于直线mx+ny+p=0对称的圆的方程,只需求出圆心关于直线的对称点即可.【典型例题5】试求圆C:x2+y2-x+2y=0关于直线l:x-y+1=0对称的曲线C′的方程.思路分析:对称圆的圆心坐标变化、半径不变,另外可利用相关点法来求.解法一:设P′(x,y)为所求曲线C′上任意一点,P′关于l的对称点为P(x0,y0),则P(x0,y0)在圆C上.由题意可得解得(*)因为P(x0,y0)在圆C上,所以x20+y20-x0+2y0=0,将(*)代入,得(y-1)2+(x+1)2-(y-1)+2(x+1)=0.化简,得x2+y2+4x-3y+5=0,即曲线C′的方程是x2+y2+4x-3y+5=0.解法二:(特殊对称)圆C关于直线l的对称图形仍然是圆,且半径不变,故只需求圆心C′,圆心C关于直线l:x-y+1=0的对称点为C′,因此所求圆C′的方程为(x+2)2+2=.