向量减法运算及其几何意义VIP免费

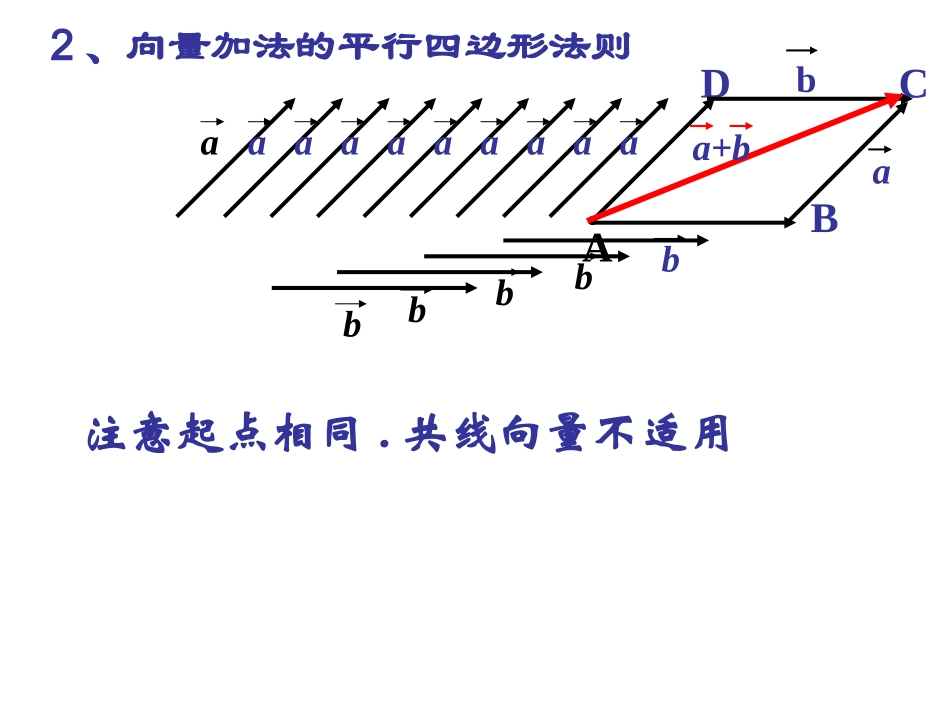
向量减法及其几何意义1、向量加法的三角形法则baOaaaaaaaabbbbbbbBbaA注意：a+b各向量“首尾相连”复习回顾复习回顾baAaaaaaaaabbbBbaDaCba+b2、向量加法的平行四边形法则注意起点相同.共线向量不适用说明：１、与长度相等、方向相反的向量，叫做的相反向量２、零向量的相反向量仍是零向量３、任一向量和它相反向量的和是零向量(),abab定义：求两个向量差的运算叫向量的减法。表示：bb探究新知探究新知一、向量减法的定义1()______(2)()_____()______(3),______,______,______aaaaaababab（）如果互为相反的向量，那么练习a00ba0(4).－AB=BA作图并总结方法。呢？作出根据减法的定义，如何已知baba,,abOAabBbCDba,,.abbaab方法：平移向量使它们起点相同，那么的终点指向的终点的向量就是结论：.二、向量减法的三角形法则OABabba特点：1、同起点2、“终点”—“起点”1.同起点2.连终点3.标方向BAOBOA向量的减法•特殊情况1.共线同向2.共线反向abBACababABCab思考1：|a－b|与|a＋b|有什么大小关系吗？为什么？|a－b|范围是多少？思考2：对于非零向量a与b，向量a＋b与a－b可能相等吗？ABCｂa＋baa－bO例1如图，已知向量aa，，bb，，cc，求作向量aa＋＋cc－－bb.ｂacAac－bDc－bBCOｂc例题分析例题分析3,,,,ABCDABaDAbOCcbcaOA����例：如图平行四边形证明：ABCDabcOOABAOBABOBacbOBCBOCOCDAcb证明：例2：化简（AB－CD）－（AC－BD）.,,.1baba求作如图，已知abaaabbb（1）（2）（3）（4）课堂练习课堂练习COBOOCOA化简.2(一)知识1．理解相反向量的概念2.理解向量减法的定义，3.正确熟练地掌握向量减法的三角形法则(二)重点重点：向量减法的三角形法则课后小节课后小节