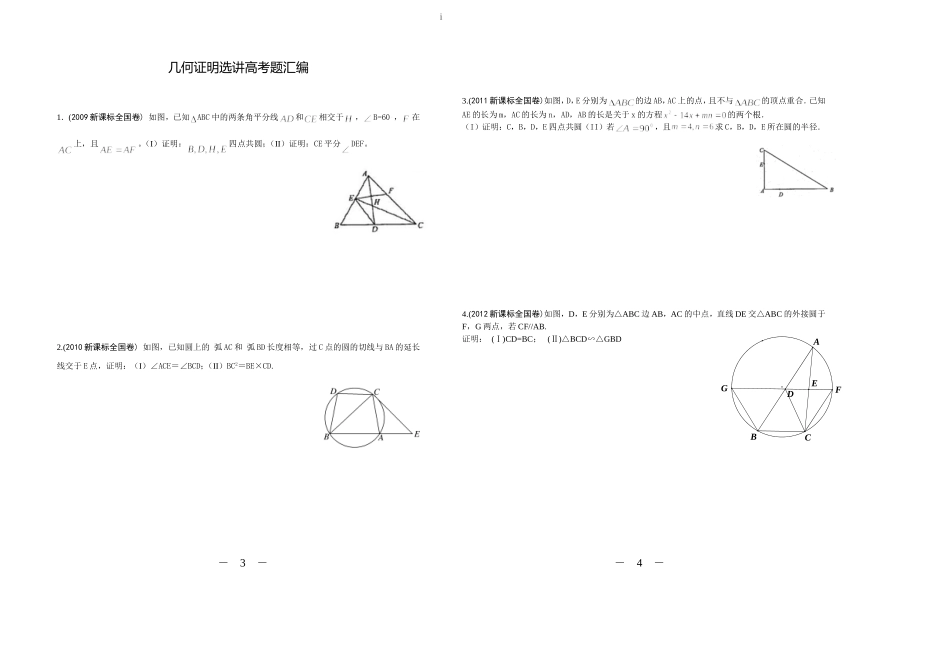
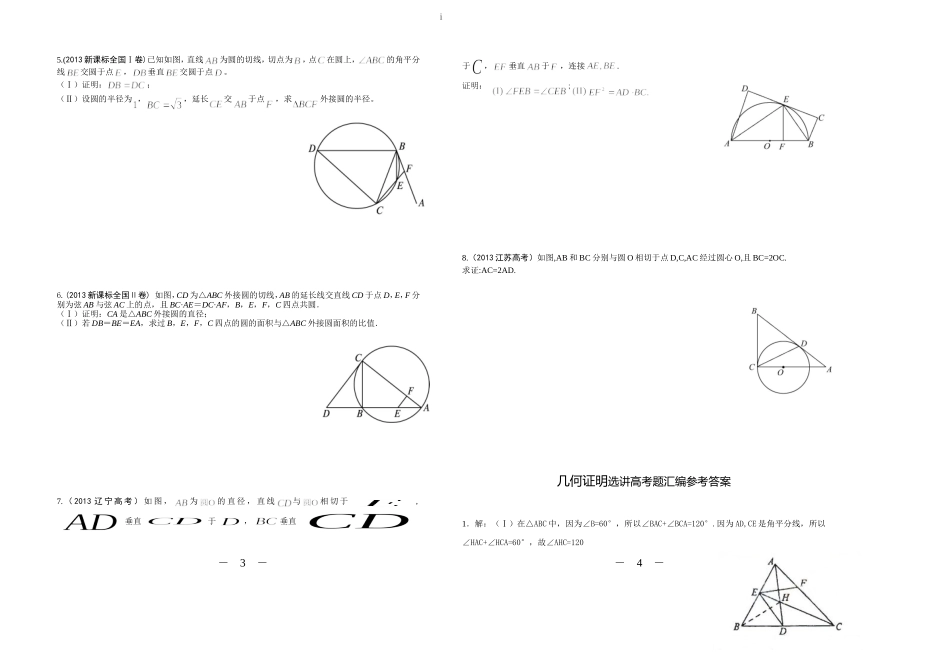
i几何证明选讲高考题汇编1.(2009新课标全国卷)如图,已知ABC中的两条角平分线和相交于,B=60,在上,且。(I)证明:四点共圆;(II)证明:CE平分DEF。2.(2010新课标全国卷)如图,已知圆上的弧AC和弧BD长度相等,过C点的圆的切线与BA的延长线交于E点,证明:(I)∠ACE=∠BCD;(II)BC2=BE×CD.3.(2011新课标全国卷)如图,D,E分别为的边AB,AC上的点,且不与的顶点重合.已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程的两个根.(I)证明:C,B,D,E四点共圆(II)若,且求C,B,D,E所在圆的半径.4.(2012新课标全国卷)如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,若CF//AB.证明:(Ⅰ)CD=BC;(Ⅱ)△BCD∽△GBD-3--4-FGDEABCi5.(2013新课标全国Ⅰ卷)已知如图,直线为圆的切线,切点为,点在圆上,的角平分线交圆于点,垂直交圆于点。(Ⅰ)证明:;(Ⅱ)设圆的半径为,,延长交于点,求外接圆的半径。6.(2013新课标全国Ⅱ卷)如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC·AE=DC·AF,B,E,F,C四点共圆.(Ⅰ)证明:CA是△ABC外接圆的直径;(Ⅱ)若DB=BE=EA,求过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值.7.(2013辽宁高考)如图,为的直径,直线与相切于,垂直于,垂直于,垂直于,连接.证明:;8.(2013江苏高考)如图,AB和BC分别与圆O相切于点D,C,AC经过圆心O,且BC=2OC.求证:AC=2AD.几何证明选讲高考题汇编参考答案1.解:(Ⅰ)在△ABC中,因为∠B=60°,所以∠BAC+∠BCA=120°.因为AD,CE是角平分线,所以∠HAC+∠HCA=60°,故∠AHC=120-3--4-i于是∠EHD=∠AHC=120°.因为∠EBD+∠EHD=180°,所以B,D,H,E四点共圆。(Ⅱ)连结BH,则BH为的平分线,得30°由(Ⅰ)知B,D,H,E四点共圆,所以30°又60°,由已知可得,可得30°所以CE平分2.解:(Ⅰ)因为弧AB,CD长度相等,所以.又因为与圆相切于点,故所以.……5分(Ⅱ)因为,,所以∽,故.即.3解:(I)连接DE,根据题意在△ADE和△ACB中,AD×AB=mn=AE×AC,即.又∠DAE=CAB∠,从而△ADEACB∽△因此∠ADE=ACB∠所以C,B,D,E四点共圆。(Ⅱ)m=4,n=6时,方程x2-14x+mn=0的两根为x1=2,x2=12.故AD=2,AB=12.取CE的中点G,DB的中点F,分别过G,F作AC,AB的垂线,两垂线相交于H点,连接DH.因为C,B,D,E四点共圆,所以C,B,D,E四点所在圆的圆心为H,半径为DH.由于∠A=900,故GHAB∥,HFAC.∥HF=AG=5,DF=(12-2)=5.故C,B,D,E四点所在圆的半径为54.解5.解:(1)证明:连结DE,交BC于点G.由弦切角定理得,∠ABE=∠BCE.而∠ABE=∠CBE,故∠CBE=∠BCE,BE=CE.又因为DB⊥BE,所以DE为直径,∠DCE=90°,由勾股定理可得DB=DC.(2)解:由(1)知,∠CDE=∠BDE,DB=DC,故DG是BC的中垂线,所以BG=.设DE的中点为O,连结BO,则∠BOG=60°.从而∠ABE=∠BCE=∠CBE=30°,所以CF⊥BF,故RtBCF△外接圆的半径等于.6.解:(1)因为CD为△ABC外接圆的切线,所以∠DCB=∠A.由题设知,故△CDB∽△AEF,所以∠DBC=∠EFA.因为B,E,F,C四点共圆,所以∠CFE=∠DBC,故∠EFA=∠CFE=90°.所以∠CBA=90°,因此CA是△ABC外接圆的直径.(2)连结CE,因为∠CBE=90°,所以过B,E,F,C四点的圆的直径为CE,由DB=BE,有CE=DC,又BC2=DB·BA=2DB2,所以CA2=4DB2+BC2=6DB2.而DC2=DB·DA=3DB2,故过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值为.7解由直线与相切于,得-3--4-i由为的直径,得,从而又垂直于,得,从而由垂直于,得又垂直于,,为公共边,所以≌,所以同理可证,≌,所以又在中,,所以综上,8证明:连结OD.因为AB和BC分别与圆O相切于点D,C,所以∠ADO=∠ACB=90°.又因为∠A=∠A,所以Rt△ADO∽Rt△ACB.所以,又BC=2OC=2OD,故AC=2AD.几何证明选讲----知识点总结1、平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等。推理1:经过三角形一边的中点与另一边平行的直线必平分第三边。推理2:经过梯形一腰的中点,且与底边平行的直线平分另一腰。平分线...