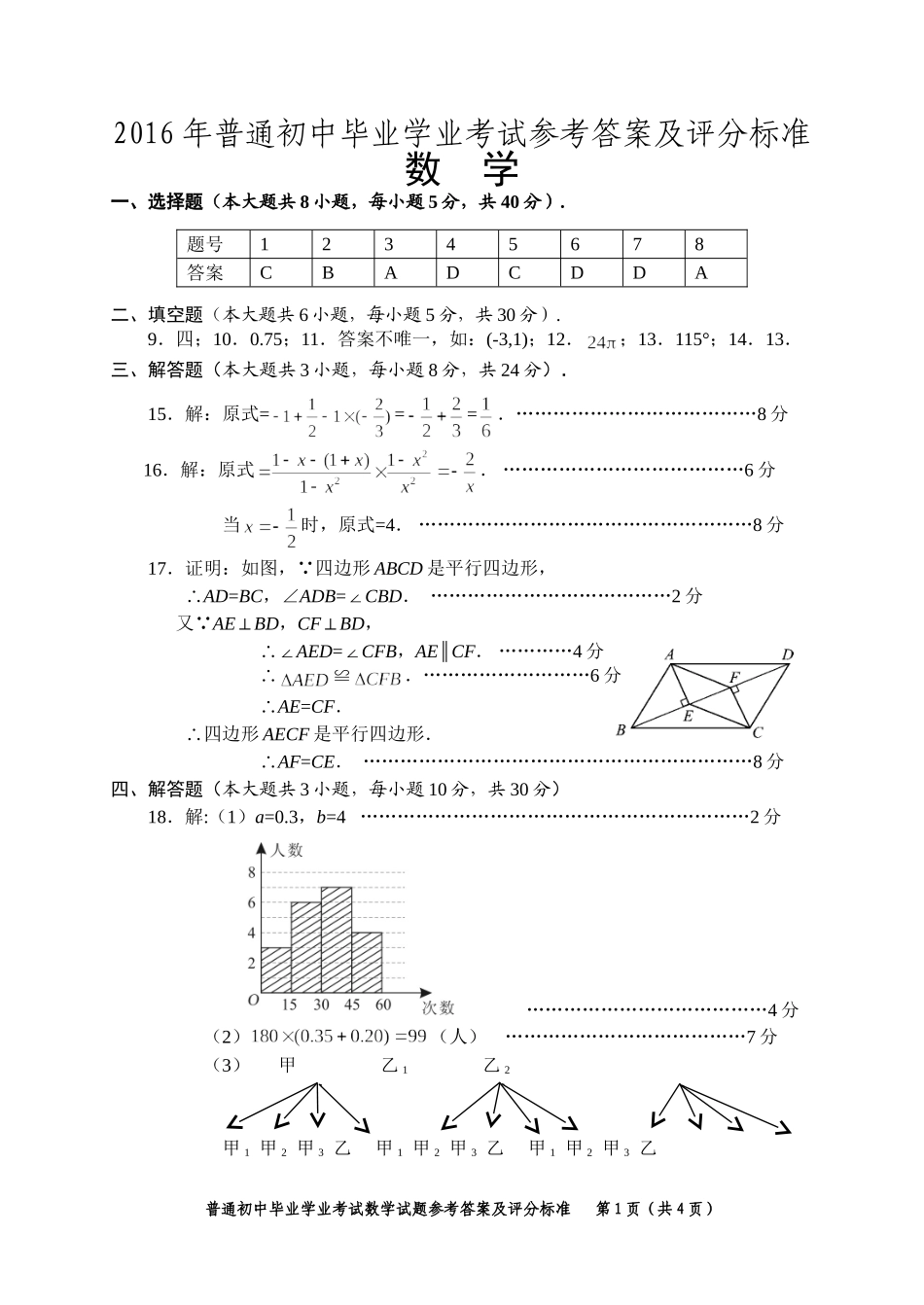
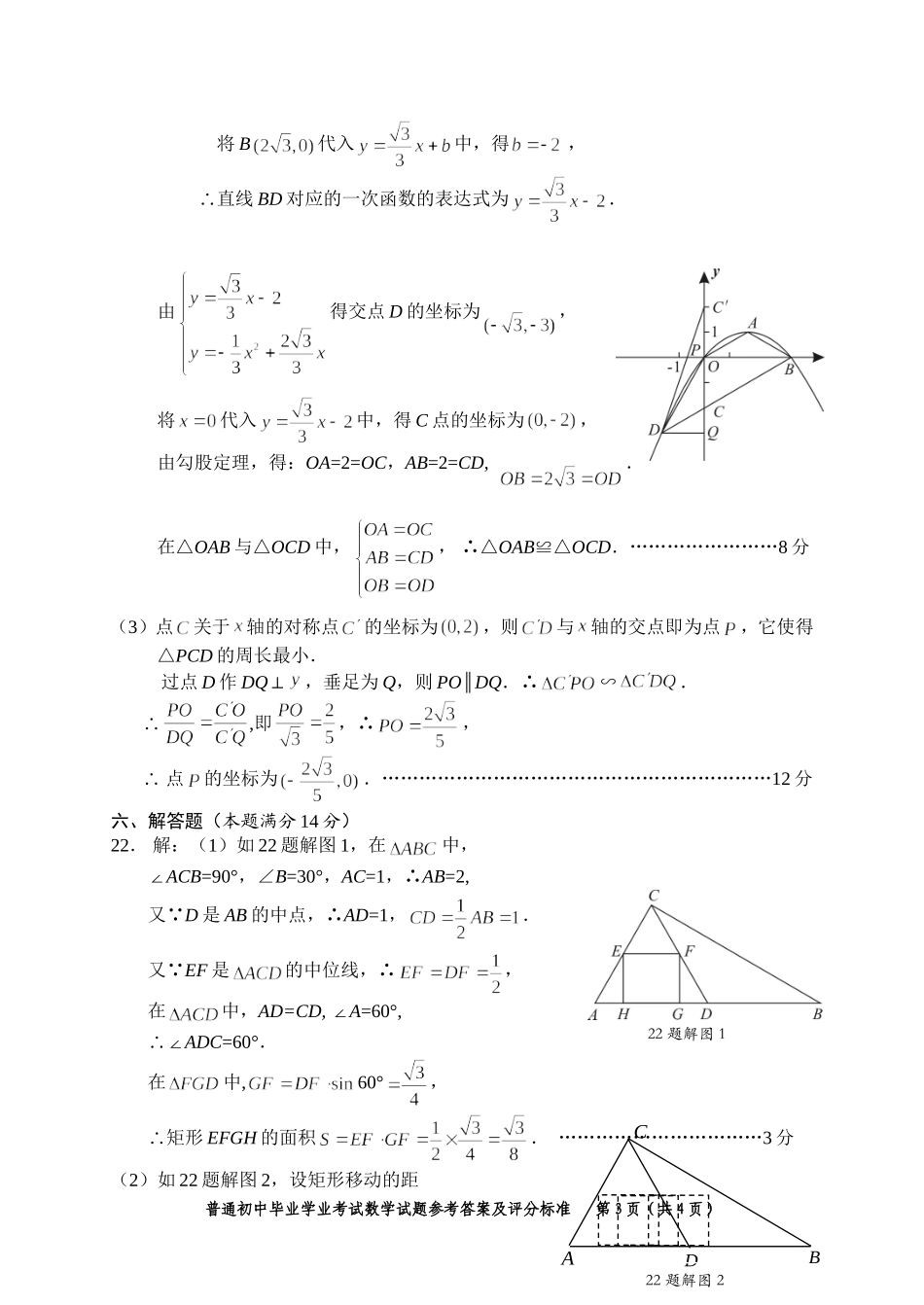
2016年普通初中毕业学业考试参考答案及评分标准数学一、选择题(本大题共8小题,每小题5分,共40分).题号12345678答案CBADCDDA二、填空题(本大题共6小题,每小题5分,共30分).9.四;10.0.75;11.答案不唯一,如:(-3,1);12.;13.115°;14.13.三、解答题(本大题共3小题,每小题8分,共24分).15.解:原式===.…………………………………8分16.解:原式.…………………………………6分当时,原式=4.………………………………………………8分17.证明:如图,∵四边形ABCD是平行四边形,∴AD=BC,∠ADB=∠CBD.…………………………………2分又∵AE⊥BD,CF⊥BD,∴∠AED=∠CFB,AE∥CF.…………4分∴≌.………………………6分∴AE=CF.∴四边形AECF是平行四边形.∴AF=CE.………………………………………………………8分四、解答题(本大题共3小题,每小题10分,共30分)18.解:(1)a=0.3,b=4………………………………………………………2分…………………………………4分(2)(人)…………………………………7分(3)甲乙1乙2甲1甲2甲3乙甲1甲2甲3乙甲1甲2甲3乙普通初中毕业学业考试数学试题参考答案及评分标准第1页(共4页)……………………………………………………………10分19.解:(1)设该班男生有人,女生有人,依题意得:,解得.∴该班男生有27人,女生有15人.…………………………………5分(2)设招录的男生为名,则招录的女生为名,依题意得:,解之得,,答:工厂在该班至少要招录22名男生.…………………………10分20.解:如图,在△ABC中,AB=15,BC=14,AC=13,设,∴.……………………………………………2分由勾股定理得:,,∴,解之得:.………………………………7分∴.………………………………………8分∴.…………10分五、解答题(本题满分12分)21.解:(1)∵抛物线顶点为,设抛物线对应的二次函数的表达式为,将原点坐标(0,0)代入表达式,得.∴抛物线对应的二次函数的表达式为:.…………3分(2)将代入中,得B点坐标为:,设直线OA对应的一次函数的表达式为,将代入表达式中,得,∴直线OA对应的一次函数的表达式为.∵BD∥AO,设直线BD对应的一次函数的表达式为,普通初中毕业学业考试数学试题参考答案及评分标准第2页(共4页)ADCB将B代入中,得,∴直线BD对应的一次函数的表达式为.由得交点D的坐标为,将代入中,得C点的坐标为,由勾股定理,得:OA=2=OC,AB=2=CD,.在△OAB与△OCD中,,∴△OAB≌△OCD.……………………8分(3)点关于轴的对称点的坐标为,则与轴的交点即为点,它使得△PCD的周长最小.过点D作DQ⊥,垂足为Q,则PO∥DQ.∴∽.∴,即,∴,∴点的坐标为.………………………………………………………12分六、解答题(本题满分14分)22.解:(1)如22题解图1,在中,∠ACB=90°,∠B=30°,AC=1,∴AB=2,又∵D是AB的中点,∴AD=1,.又∵EF是的中位线,∴,在中,AD=CD,∠A=60°,∴∠ADC=60°.在中,60°,∴矩形EFGH的面积.……………………………3分(2)如22题解图2,设矩形移动的距普通初中毕业学业考试数学试题参考答案及评分标准第3页(共4页)22题解图1CADB22题解图2离为则,当矩形与△CBD重叠部分为三角形时,则,,∴.(舍去).当矩形与△CBD重叠部分为直角梯形时,则,重叠部分的面积S=,∴.即矩形移动的距离为时,矩形与△CBD重叠部分的面积是.…………8分(3)如22题解图3,作于.设,则,又,.在Rt△H2QG1中,,解之得(负的舍去).∴.……………………………………14分普通初中毕业学业考试数学试题参考答案及评分标准第4页(共4页)1H1E1F1GCA2H2E2FDB22题解图31H1E1F1GCA2H2E2FDBQ