信息技术应用_借助信息技术探究指数函数的性质VIP免费

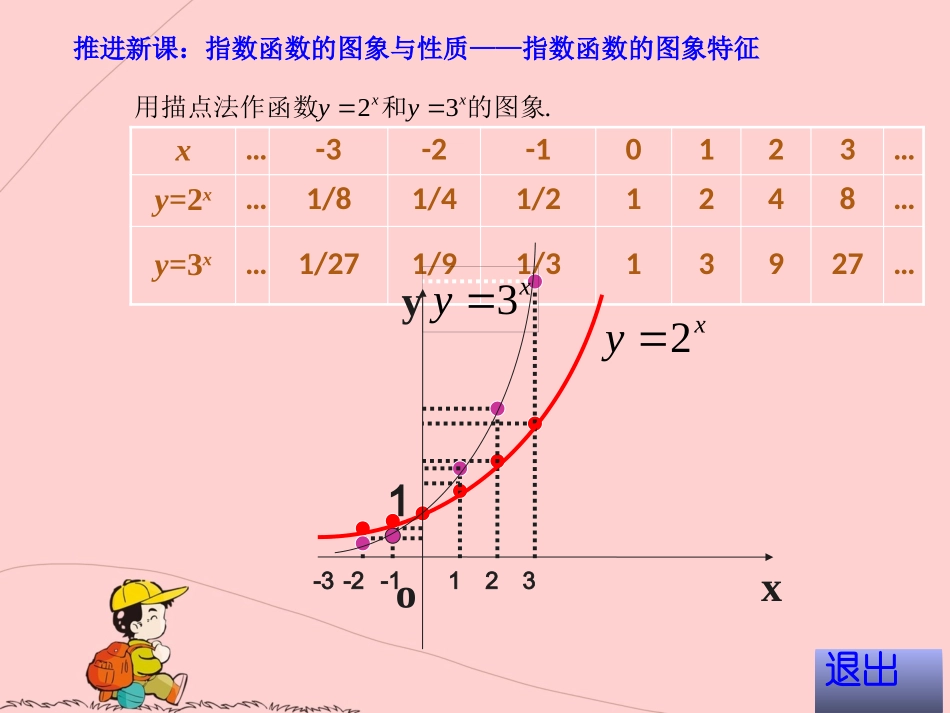
指数函数的图象与性质车胤中学：周玄退出二、定义辨析1：指出下列函数哪些是指数函数？.1,21,128,7,6,544,43,2,414aaayxyyyyyxyyxxxxxx且指数函数的图象与性质——复习巩固一、复习提问：指数函数的定义一般地，函数y=ax(a>0且a≠1)叫指数函数，其中x是自变量，函数的定义域是R.答：（1），（5），（6），（8）是指数函数。.32的图象和用描点法作函数xxyyx…-3-2-10123…y=2x…1/81/41/21248…y=3x…1/271/91/313927…1xy2xy3推进新课：指数函数的图象与性质——指数函数的图象特征退出xyo123-1-2-3x…-3-2-10123…y=2-x…84211/21/41/8…y=3-x…279311/31/91/27…XOYY=1.)31()21(的图象和用描点法作函数xxyyxy)21(xy)31(指数函数的图象与性质——函数图象特征退出观察右边图象，回答下列问题：问题一：图象分别在哪几个象限？问题二：图象的上升、下降与底数a有联系吗？问题三：图象过哪个特殊的点？答:四个图象都在第＿＿＿＿象限。答：当底数＿＿时图象上升；当底数＿＿时图象下降．答：四个图象都经过点＿＿＿＿．Ⅰ、Ⅱ1a>01a<<)1,0(指数函数的图象和性质——图象特征下页XOYY=1y=3Xy=2xxy21xy31图象性质(0,1)y=ax(a>1)x(0,1)y=1y=ax(0100时，y>1.当x<0时，y>1；当x>0时，01)x(0,1)y=1y=ax(0100时，y>1.当x<0时，y>1；当x>0时，00,a≠1）中a的变化会引起函数图象怎样的变化呢？指数函数的图象与性质——课堂练习.21,8,429315.134.029.0122yyyyx、比较大小：的定义域。、求函数的取值范围。求实数，，的定义域是、若函数aayx013的取值范围。求实数恒成立，时，、当aaxx11042指数函数的图象与性质——课堂探究一、底数a对指数函数图象的影响。二、如何解指数型不等式：的解集。且的不等式、求关于)10(11472aaaaxxx.2122131)10(,2yyxaaayayxx的范围，使确定且、已知三、如何求指数型函数的值域：3232112221)4(2)3(,2)2(,2)1(xxxxxxyyyy求下列函数的值域：1.0001(0.9999)xxyy与3651.0137.8y3650.990.03y“积跬步以致千里，积怠惰以致深渊”3651.021377.4y3650.980.0006y“只比你努力一点的人，其实已经甩你很远”