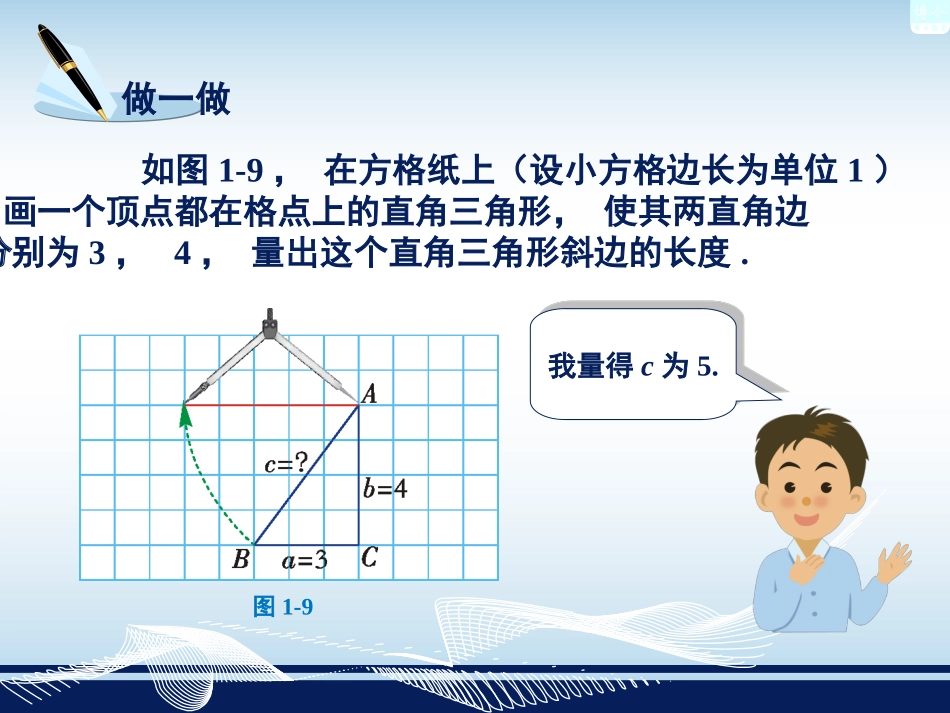
直角三角形的性质和判定(Ⅱ)本课内容本节内容1.2做一做如图1-9,在方格纸上(设小方格边长为单位1)画一个顶点都在格点上的直角三角形,使其两直角边分别为3,4,量出这个直角三角形斜边的长度.图1-9我量得c为5.我量得c为5.议一议议一议议一议议一议议一议议一议在方格纸上,以图1-9中的Rt△ABC的三边为边长分别向外作正方形,得到三个大小不同的正方形,如图1-10,那么这三个正方形的面积S1,S2,S3之间有什么关系呢?图1-10议一议议一议议一议议一议议一议议一议由图1-10可知,S1=32,S2=42,为了求S3,我可以先算出红色区域内大正方形的面积,再减去4个小三角形的面积,得S3=52. 32+42=52,∴S1+S2=S3.在图1-10中,S1+S2=S3,即BC2+AC2=AB2,那么是否对所有的直角三角形,都有两直角边的平方和等于斜边的平方呢?图1-10探究如图1-11,任作一个Rt△ABC,∠C=90°,若BC=a,AC=b,AB=c,那么a2+b2=c2是否成立呢?图1-11步骤1先剪出4个如图1-11所示的直角三角形,由于每个直角三角形的两直角边长为a,b(其中b>a),于是它们全等(SAS),从而它们的斜边长相等.设斜边长为c.图1-11我们来进行研究.步骤2再剪出1个边长为c的正方形,如图1-12所示.图1-12步骤3把步骤1和步骤2中剪出来的图形拼成如图1-13的图形.图1-13由于△DHK△EIH,∴∠2=∠4.又 ∠1+2=90°∠,∴∠1+4=90°.∠因此拼成的图形是正方形DEFG,它的边长为(a+b),它的面积为(a+b)2.又∠KHI=90°,∴∠1+∠KHI+4=180°∠,即D,H,E在一条直线上.图1-13同理E,I,F在一条直线上;F,J,G在一条直线上;G,K,D在一条直线上.又正方形DEFG的面积为c2+,142·ababcab.221()42∴即a2+2ab+b2=c2+2ab,∴a2+b2=c2.图1-13结论直角三角形两直角边a,b的平方和,等于斜边c的平方.a2+b2=c2直角三角形两直角边a,b的平方和,等于斜边c的平方.a2+b2=c2由此得到直角三角形的性质定理:其实我国早在三千多年前就已经知道直角三角形的上述性质,由于古人称直角三角形的直角边中较短的一边为勾,较长的一边为股,斜边为弦(如图1-14),因此这一性质被称为勾股定理.勾股定理揭示了直角三角形三边之间的关系.在直角三角形中,若已知直角三角形任意两条边长,我们可以根据勾股定理,求出第三边的长.勾股弦故AD的长为12cm.在Rt△ADB中,由勾股定理得AD2+BD2=AB2,如图1-15,在等腰三角形ABC中,已知AB=AC=13cm,BC=10cm,AD⊥BC于点D.你能算出BC边上的高AD的长吗?例1图1-15举例解在△ABC中, AB=AC=13,BC=10,AD⊥BC,∴BD==5.BC12222213518812.ADABBD∴在Rt△ABC中,∠C=90°.(1)已知a=25,b=15,求c;(2)已知a=5,c=9,求b;(3)已知b=5,c=15,求a.练习答:(1)c=;(2);(3)534b214a.102动脑筋如图1-16,电工师傅把4m长的梯子AC靠在墙上,使梯脚C离墙脚B的距离为1.5m,准备在墙上安装电灯.当他爬上梯子后,发现高度不够,于是将梯脚往墙脚移近0.5m,即移动到C′处.那么,梯子顶端是否往上移动0.5m呢?图1-16在Rt△ABC中,AC=4m,BC=1.5m,图1-17由勾股定理得,(m).224151375371AB...图1-16由图1-16抽象出示意图1-17.在Rt△ABC中,计算出AB;再在Rt△中,计算出,则可得出梯子往上移动的距离为(-AB)m.ABCABAB即梯子顶端A点大约向上移动了0.16m,而不是向上移动0.5m.图1-17因此=3.87-3.71=0.16(m).AA在Rt△中,=4m,=1m,故224115387mAB..()ACABCBC(“引葭赴岸”问题)“今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”意思是:有一个边长为10尺的正方形池塘,一棵芦苇生长在池的中央,其出水部分为1尺.如果将芦苇沿与水池边垂直的方向拉向岸边,它的顶端恰好碰到池边的水面.问水深与芦苇长各为多少?例2宋刻《九章算术》书影举例分析根据题意,先画出水池截面示意图,如图1-18.设AB为芦苇,BC为芦苇出水部分,即1尺,将芦苇拉向岸边,其顶部B点恰好碰到岸边B′.在Rt△ACB′中,根据勾股定理,得x2+52=(x+1)2,答:水池的深度为12尺,芦苇长为13尺.如图1-18,设水池深为x尺,则AC=x尺,AB=AB′=(x+1)尺.解...