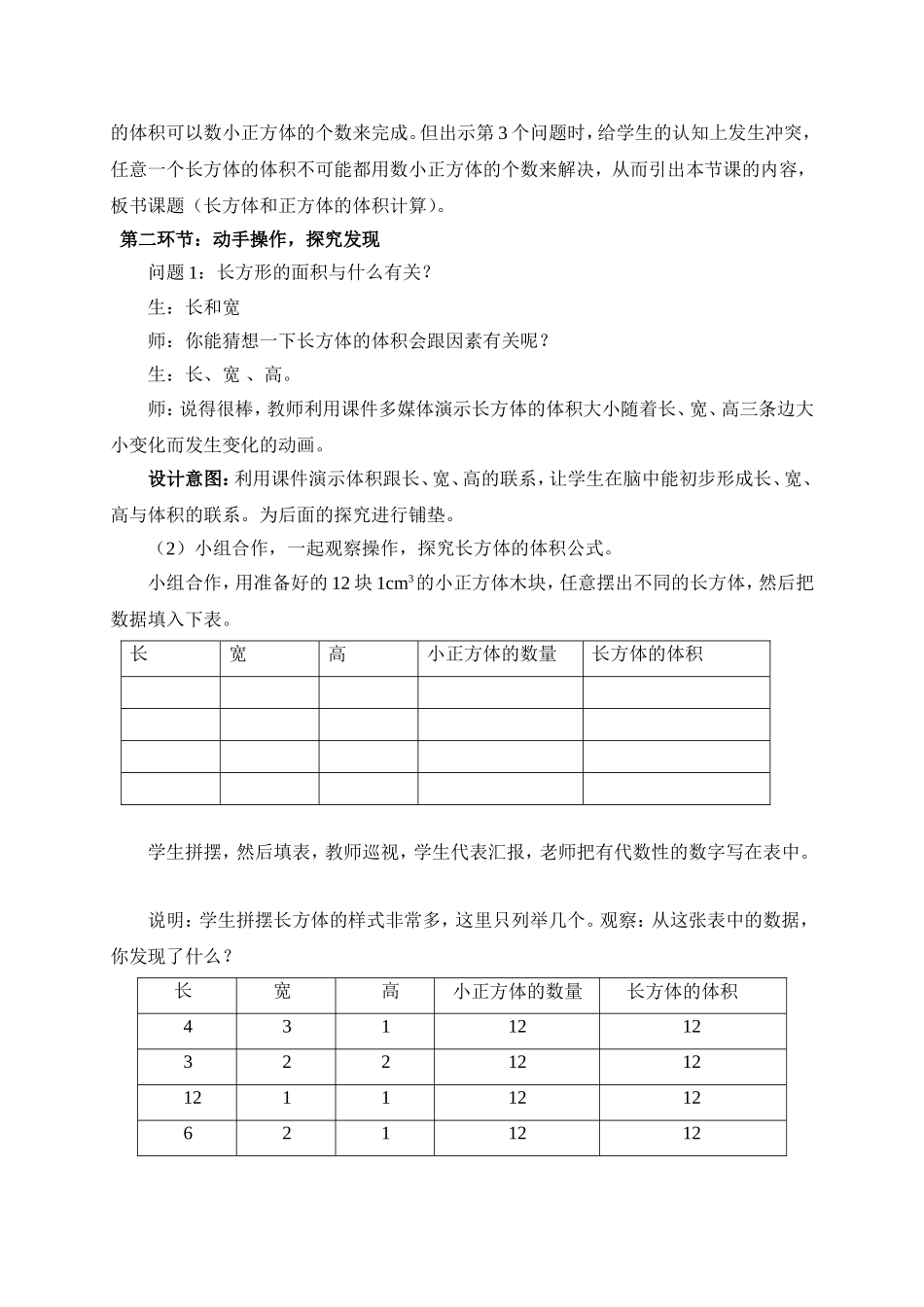
《长方体和正方体的体积》教学案例詹天佑小学汪万荣教学内容课程标准实验教科书(人教版)小学数学五年级下册《长方体、正方体的体积计算》,第1个课时。教材分析:《长方体和正方体的体积》是《数学课程标准》“空间与图形”领域中“图形的认识”的重要内容,这一部分是在学生掌握了长方体和正方体的表面积的相关知识的基础之上而安排的内容。也是学生从平面图形过渡到立体图形的一个重要内容,进一步学习有关它的知识,也是为学习其它立体图形的体积计算打下良好的基础。学情分析:五年级的学生,学习的主观性和能动性都有了较大的提高,同时,他们的思维能力、分析能力、动手操作能力、语言表达能力都有所发展。在几何图形的学习中,学生最感兴趣的是动手操作,亲自实践,所以本节课的教学应着重让学生自主探究,合作交流,动手实践,让学生在具体实践中亲自体验,感知长方体体积的计算公式的推导过程。学习目标1.认知目标:通过小组合作探究动手操作等方式推导出长方体、正方体的体积公式。2.能力目标:能熟悉运用长方体和正方体的体积计算公式解决实际问题。3.情感目标:培养和发展学生的空间观念,培养学生逻辑推理能力。教学重点:长方体、正方体体积计算。教学难点:长方体体积计算公式的推导教、学具准备:体积为1立方厘米的正方体积木12个,多媒体课件。教学过程:第一环节:复习提问,情境导入1.什么叫物体体积?计量物体的体积常用的单位有哪些?2.教师出示课件,下面的图形都是由棱长为1厘米的小正方体拼成的,它们的体积各是多呢?你是怎样想的?(学生思考)。3.出示任意一个长方体,你能知道它的体积是多少吗?设计意图:通过复习旧知,让学生回忆上节课的内容,为本节课的内容打下基础,让学生从棱长为1厘米的正方体体积是1立方厘米引出思考,由小正方体组成的立体图形的体积可以数小正方体的个数来完成。但出示第3个问题时,给学生的认知上发生冲突,任意一个长方体的体积不可能都用数小正方体的个数来解决,从而引出本节课的内容,板书课题(长方体和正方体的体积计算)。第二环节:动手操作,探究发现问题1:长方形的面积与什么有关?生:长和宽师:你能猜想一下长方体的体积会跟因素有关呢?生:长、宽、高。师:说得很棒,教师利用课件多媒体演示长方体的体积大小随着长、宽、高三条边大小变化而发生变化的动画。设计意图:利用课件演示体积跟长、宽、高的联系,让学生在脑中能初步形成长、宽、高与体积的联系。为后面的探究进行铺垫。(2)小组合作,一起观察操作,探究长方体的体积公式。小组合作,用准备好的12块1cm3的小正方体木块,任意摆出不同的长方体,然后把数据填入下表。长宽高小正方体的数量长方体的体积学生拼摆,然后填表,教师巡视,学生代表汇报,老师把有代数性的数字写在表中。说明:学生拼摆长方体的样式非常多,这里只列举几个。观察:从这张表中的数据,你发现了什么?长宽高小正方体的数量长方体的体积43112123221212121112126211212学生独立思考,然后小组内讨论交流,得出结论。小结:长方体的体积等于长方体所含体积单位的数量,所含体积单位的数量正好等于长方体长、宽、高的乘积。板书:长方体的体积=长×宽×高讲述:如果用字母V表示长方体的体积,用a、b、h分别表示长方体的长、宽、高,那么长方体的体积计算公式可以写成:V=abh(3)质疑:求长方体的体积公式需要知道什么条件?学生思考后回答,(长、宽、高)设计意图:通过学生动手操作、小组合作的方式推导出长方体的体积公式,让学生感觉出新知识不难,实现平稳过渡,使学生树立学习新知识,解决新问题的信心。2.探究正方体的体积公式。(1)请大家想一想,根据正方体与长方体的关系,联系长方体体积公式,想一想正方体的体积应该怎样计算。组内讨论,交流。汇报:正方体是长、宽、高都相等的长方体,所以正方体的体积=棱长×棱长×棱长(板书)用字母表示:V=a·a·a=a3(a表示棱长)(a3读作a的立方,表示3个a相乘)3.运用长方体的体积公式解决问题。例1:一个长方体的长7cm,宽4cm,高3cm,它的体积是多少?例2:一块正方体石料,棱长是6dm,这块石料的体积是多少立方分...