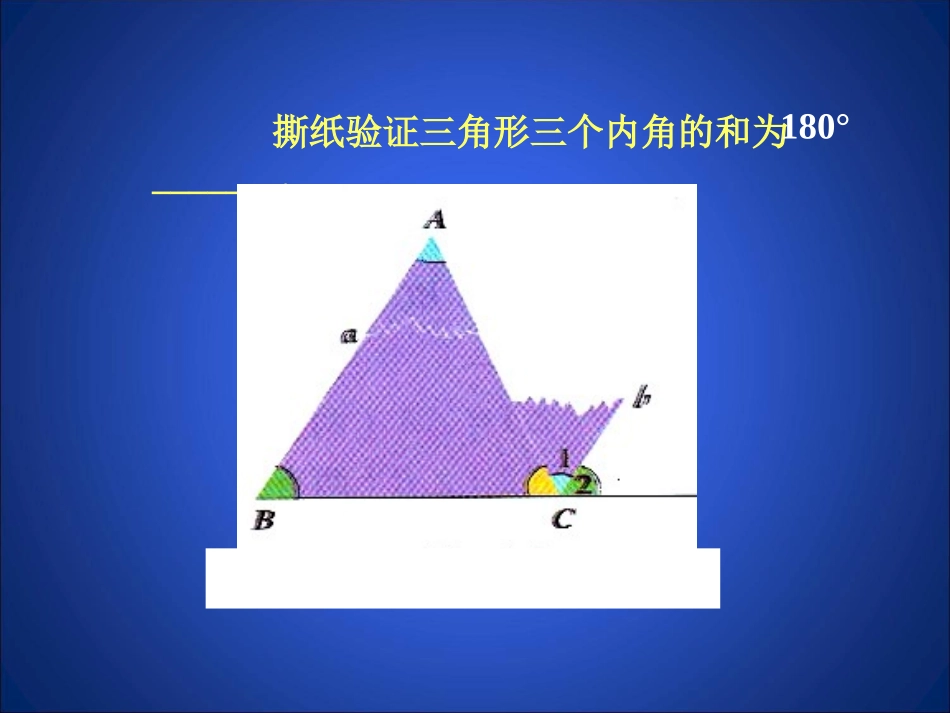
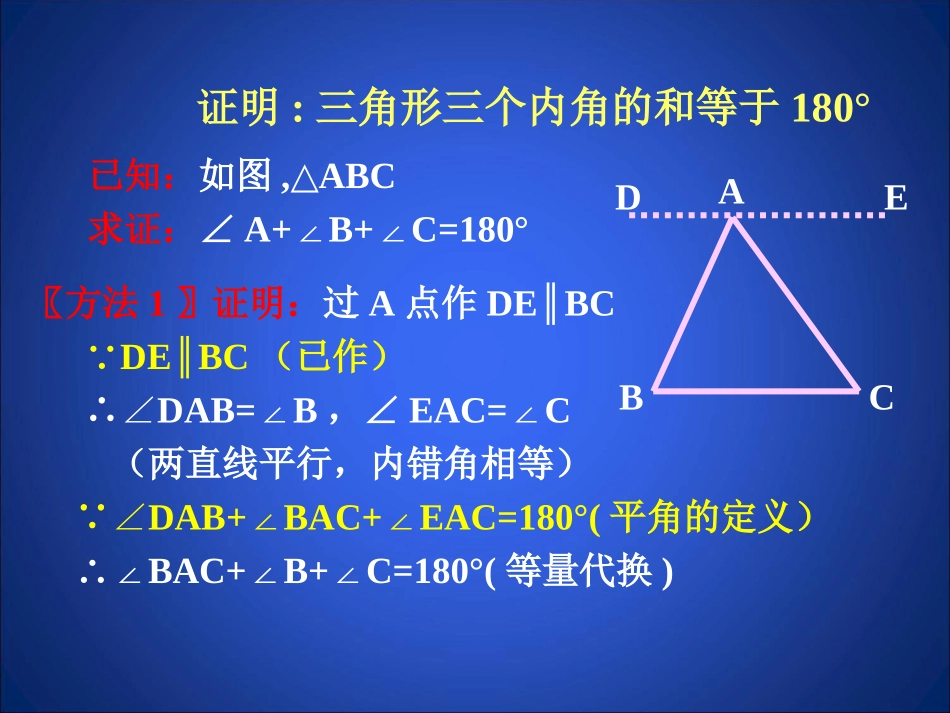
5.三角形内角和定理(第1课时)第七章平行线的证明撕纸验证三角形三个内角的和为_______.180°证明:三角形三个内角的和等于180°已知:如图,ABC△求证:∠A+B+C=180°∠∠BACED〖方法1〗证明:过A点作DEBC∥∵DEBC∥(已作)∴∠DAB=B∠,∠EAC=C∠(两直线平行,内错角相等)∵∠DAB+BAC+EAC=180°(∠∠平角的定义)∴∠BAC+B+C=180°(∠∠等量代换)证明:三角形三个内角的和等于180°已知:如图,ABC△求证:∠A+B+C=180°∠∠BAC〖方法2〗证明:作BC的延长线CD,过点C作射线CEBA∥。∵CEBA∥∴∠B=ECD∠(两直线平行,同位角相等)∠A=ACE∠(两直线平行,内错角相等)∵∠BCA+ACE+ECD=180°(∠∠平角的定义)∴∠A+B+ACB=180°(∠∠等量代换)ED例1.如图,在△ABC中,∠B=38°,∠C=63°AD是△ABC的平分线,求∠ADB的度数.DCBA练一练1.△ABC中,∠C=90°,∠A=30°,∠B=?2.∠A=50°,∠B=∠C,则△ABC中∠B=?3.△ABC中可以有3个锐角吗?3个直角呢?2个直角呢?若有1个直角,另外两角有什么特点?4.三角形的三个内角中,只能有__个直角或__个钝角5.任意一个三角形,至少有__个锐角,至多有__个锐角6.三角形中三角之比为1∶2∶3,则三个角各为多少度?7.已知:△ABC中,∠C=B=2A∠∠(a)求∠B的度数(b)若BD是AC边上的高,求∠DBC的度数.CBAD今天的收获证明三角形内角和定理的几种方法三角形内角和定理的简单应用辅助线的作法技巧今天的作业课本随堂练习;习题