高2017届综合练习（一）VIP免费

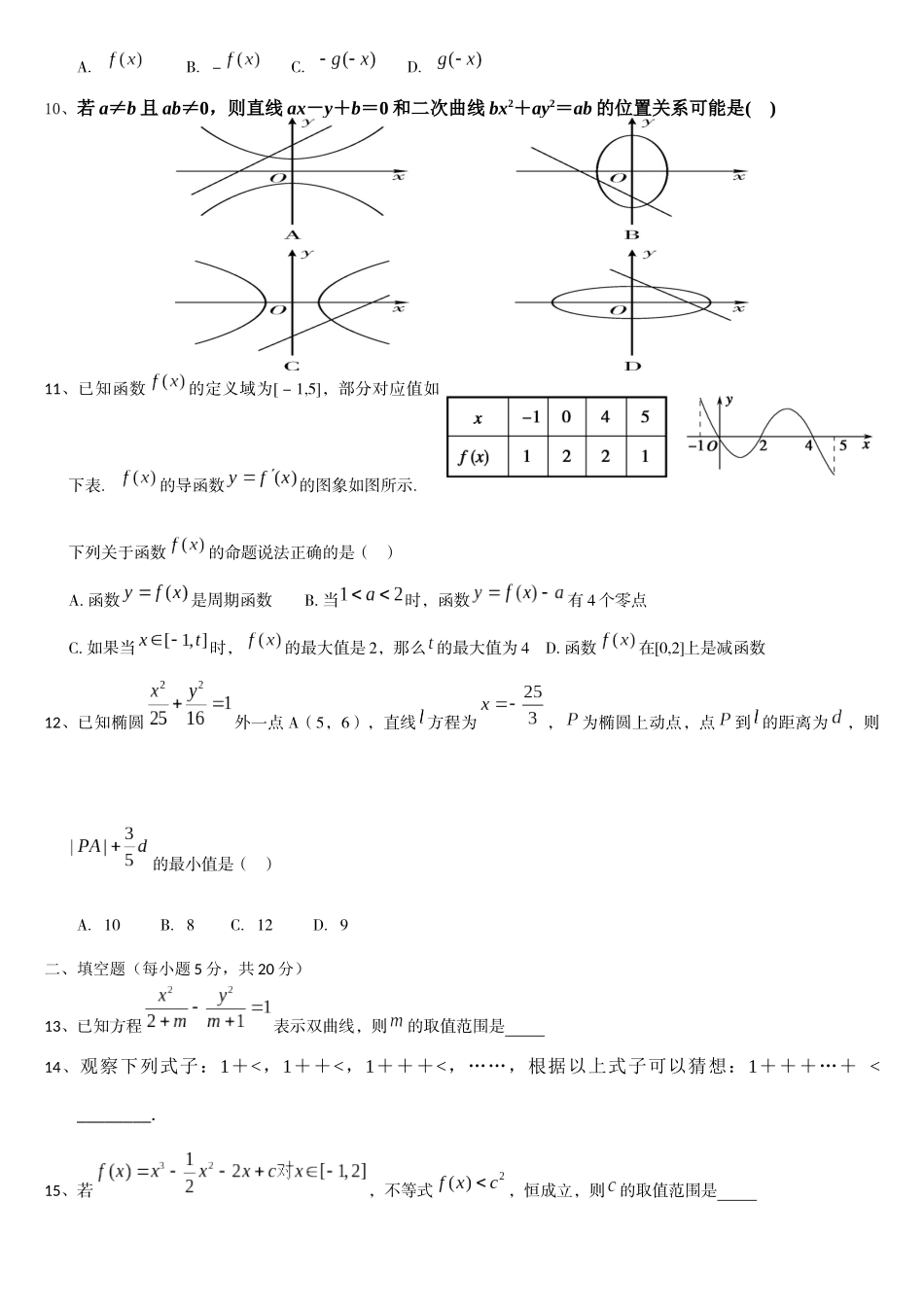
高2017届综合练习（一）一、选择题（每小题5份，共60分）1、“所有金属都能导电，铁是金属，所以铁能导电。”这种推理属于（）A．类比推理B．合情推理C．归纳推理D.演绎推理2、命题“,”的否定是（）（A）,（B），（C）,（D），3、复数在复平面内对应的点的坐标为（）A．（0,1）B．（0，-1）C．（-1,0）D．（1,0）4、“”是“”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件5、执行下面的框图，若输入的是6，则输出的值是（）A．120B.720C．1440D．50406、曲线与曲线（）的（）A.长轴长相等B.短轴长相等C.焦距相等D.离心率相等7、函数()(23)xfxxe的单调递增区间是（）A.1(,)2B.1(,)2C.1(0,)2D.(2,)8、设是椭圆的两个焦点,若椭圆上存在点,使,则椭圆离心率的取值范围是（）A．B．C．D．9、观察，则归纳推理可得，若定义在上的函数满足为的导数，则=（）A．B．-C．D．10、若a≠b且ab≠0，则直线ax－y＋b＝0和二次曲线bx2＋ay2＝ab的位置关系可能是()11、已知函数的定义域为[－1,5]，部分对应值如下表．的导函数的图象如图所示．下列关于函数的命题说法正确的是（）A.函数是周期函数B.当时，函数有4个零点C.如果当时，的最大值是2，那么的最大值为4D.函数在[0,2]上是减函数12、已知椭圆外一点A（5，6），直线方程为，为椭圆上动点，点到的距离为，则的最小值是（）A．10B．8C．12D．9二、填空题（每小题5分，共20分）13、已知方程表示双曲线，则的取值范围是14、观察下列式子：1＋<，1＋＋<，1＋＋＋<，……，根据以上式子可以猜想：1＋＋＋…＋<________.15、若，不等式，恒成立，则的取值范围是16、德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数被称为狄利克雷函数,其中为实数集，为有理数集，则关于函数有如下四个命题：①函数是偶函数；②；③任取一个不为零的有理数对任意的恒成立；④不存在三个点.使得为等边三角形.其中为真命题的是高2017届综合练习（一）一、选择题（每小题5分，共60分）123456789101112二、填空题（每小题5分，共20分）13、14、15、16、三、解答题（17题10分，其余各小题每小题12分，共70分）17、已知：求证：中至少有一个小于2.18、已知命题p：方程y24−t+x2t−8=1表示焦点在y轴上的双曲线；命题q：实数t使函数f(x)=log2(x2−2tx+2t+3)的定义域是R．（Ⅰ）若2t时，求命题p中的双曲线的离心率及渐近线方程；（Ⅱ）求命题¬p是命题¬q的什么条件(充分不必要，必要不充分，充要，既不充分又不必要中的一种)，并说明理由．19、下图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图.注：年份代码1–7分别对应年份2008–2014.（Ⅰ）由折线图看出，可用线性回归模型拟合y与t的关系，请用相关系数加以说明；（Ⅱ）建立y关于t的回归方程（系数精确到0.01），预测2016年我国生活垃圾无害化处理量.附注：参考数据：719.32iiy，7140.17iiity，721()0.55iiyy，≈2.646.参考公式：12211()()()(yy)niiinniiiittyyrtt，回归方程yabt中斜率和截距的最小二乘估计公式分别为：121()()()niiiniittyybtt，=.aybt20、某产品生产厂家生产一种产品，每生产这种产品x（百台），其总成本为G(x)（万元），其中固定成本为42万元，且每生产1百台的生产成本为15万元（总成本固定成本生产成本）．销售收入R(x)（万元）满足假定该产品产销平衡（即生产的产品都能卖掉），根据上述规律，完成下列问题：（1）写出利润函数y=f(x)的解析式（利润销售收入总成本）；（2）要使工厂有盈利，求产量x的范围；（3）工厂生产多少台产品时，可使盈利最大？21、已知函数f(x)=−x2+2blnx,g(x)=x+1x，两函数有相同极值点（1）求实数b的值；（2）若对于（为自然对数的底数），不等式恒成立，求实数的取值范围．22、如图，为坐标原点，椭圆（）的左、右焦点分别为，离心率为；双曲线的左、右焦点分别为，离心率为.已知，且.（Ⅰ）求的方程；（Ⅱ）过作的不垂直于轴的弦，为的中点．当直线与交于两点时，求四边形面积的最小值．