集合的基本运算（二）VIP免费

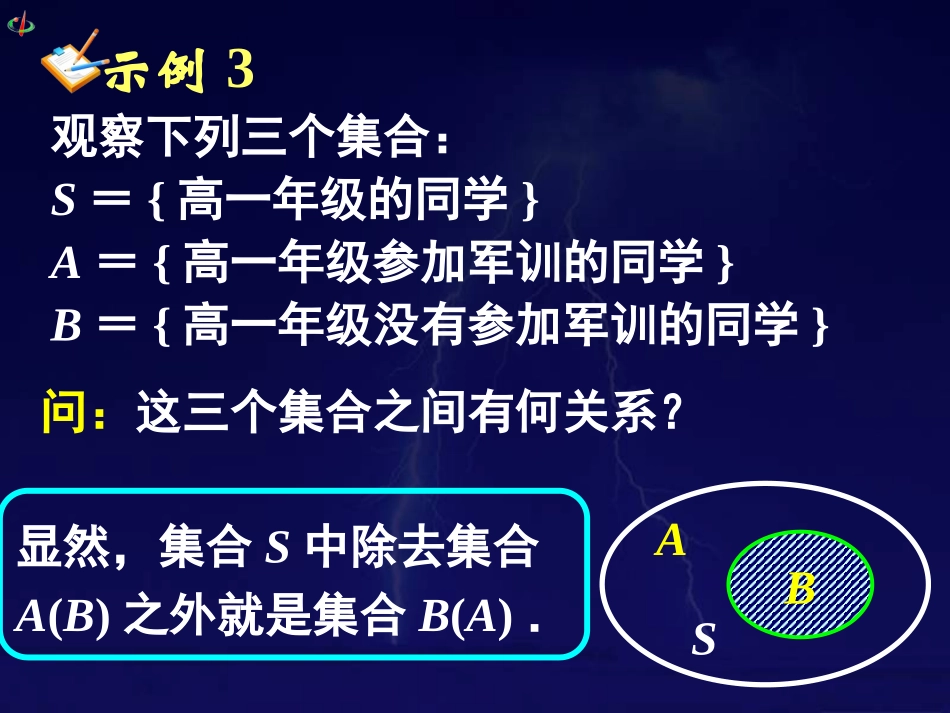
示例3观察下列三个集合：S＝{高一年级的同学}A＝{高一年级参加军训的同学}B＝{高一年级没有参加军训的同学}问：这三个集合之间有何关系？显然，集合S中除去集合A(B)之外就是集合B(A)．ASB一般地，设S是一个集合，A是S中的一个子集，即AS，则由S中所有不属于A的元素组成的集合，叫做S中集合A的补集，补集记作:SASA.即＝{x|x∈S，且xA}.SASA1.S＝{1，2，3，4，5，6},A＝{1，3，5}{2，4，6}.则SASA＝2.设集合S＝{x|－1＜x＜2},A＝{x|1＜x＜2}.则SASA＝{x|-1＜x1}.3.设集合A＝{x|x＜2或x3},ACR则{x|2x<3}.所要研究的各个集合的全部元素所组成的集合叫做全集.研究补集必须是在全集的条件下研究，而全集因研究问题不同而异，全集常用U来表示．注意：补集性质1：若全集为U，AU，则⑶UUUU⑴U=⑵U)(AUU)(AUUA拓展引申.设集合U＝R,A={x|－1＜x2},B＝{x|1x＜5}.BCACBACUUU),(.1求BCACBACUUU),(.2求补集性质2：BCACBACUUU)(BCACBACUUU)(例1填空题．⑴若S＝{2,3,4}，A＝{4,3}，则＝.⑵若S＝{三角形}，B＝{锐角三角形}，则＝．⑶若S＝{1,2,4,8}，A＝，则＝.⑷已知A＝{0,2,4}，＝{－1,1}，＝{－1,0,2}，则B＝.SASASBSBSASAUAUAUBUB例2在下列各组集合中，U为全集，A为U的子集，求．⑴U＝R，A＝{x|－1≤x2}⑵U＝Z，A＝{x|x＝3k，k∈Z}UAUA例3已知全集U＝{2，3，a2＋2a－3}A＝{|2a－1|，2}，若＝{5}，求实数a的值．UAUA拓展提升例4设全集为U=R，集合M＝{x|3a-1