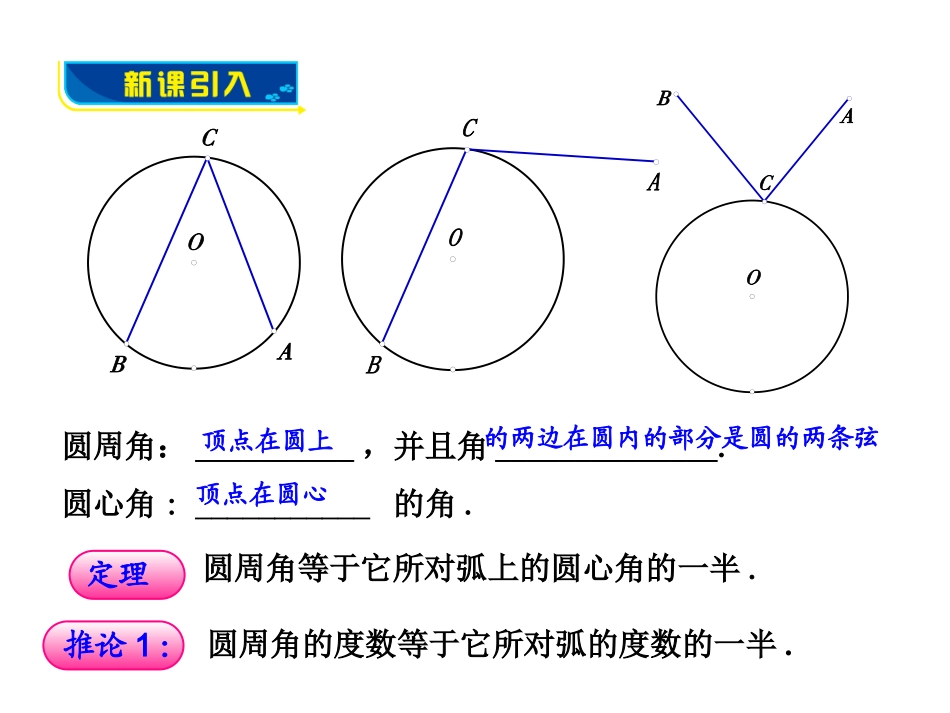
3.3圆周角第2课时1.掌握圆周角定理的推论2和推论3及简单应用;2.渗透由“特殊到一般”,由“一般到特殊”的数学思想方法.圆周角:__________,并且角______________.圆心角:___________的角.顶点在圆上的两边在圆内的部分是圆的两条弦顶点在圆心圆周角等于它所对弧上的圆心角的一半.定理推论1:圆周角的度数等于它所对弧的度数的一半.OBCAOCABOBAC如图,劣弧与的度数之差为20°,弦AB与CD交于点E,∠CEB=60°.求∠CAB的度数.热身EABC解在△ACE中,∵∠CEB=∠CAB+∠ACD,∠CAB的度数=的度数,∠ACD的度数=的度数,∠CEB=60°,∴的度数+的度数=∠CAB的度数+∠ACD的度数=∠CEB的度数=60°.∵的度数-的度数=20°,∴的度数=70°.∴∠CAB的度数=的度数=170352DABC1OC2C3在⊙O中,∠C1,∠C2,∠C3都是所对的圆周角,它们的大小有什么关系?相等理由?圆周角的度数等于它所对弧的度数的一半.同弧上的圆周角相等;相等的圆周角所对的弧相等.FED牢记:1,“同圆或等圆”的条件不能去掉?2,弧﹤=﹥圆周角推论2:OCBA反过来说对吗?图3—27或等弧在同圆或等圆中,直径所对的圆周角是90°;90°的圆周角所对的弦是直径.推论3:OBADEC提示:以后需要直角时先看看有木有直径!例题例2如图,△ABC内接于⊙o,A为劣弧BC的中点,∠BAC=1200.过点B作⊙O的直径,连接AD.若AD=6,求AC的长.例3如图,AD是△ABC的高,AE是△ABC外接圆直径,点O为圆心.△ADC与△ABE相似吗?说明理由.CABEDO解△ADC∽△ABE.理由如下:∵AE为⊙O的直径,∴∠ABE=90°.∵AD⊥BC,∴∠ADC=90°.∠ADC=∠ABE.∵∠ACD=∠AEB,△ADC∽△ABE.例题•课后练习挑战自我如图,AB是⊙O的直径,E为⊙O上一点,C是弧AE的中点.CDAB⊥,垂足为点D.AE交CD于点E,连接AC.求证:AF=CF.1、如图,在⊙O中,∠ABC=50°,则∠AOC等于().A.50°B.80°C.90°D.100°ACBOD2、如图,△ABC是等边三角形,动点P在圆周的劣弧AB上,且不与A、B重合,则∠BPC等于().A.30°B.60°C.90°D、45°CABPB跟踪训练·1.如图,∠A=50°,∠ACB=60°BD是⊙O的直径,则∠AEB等().A.70°B.100°C.90°D.120°BACBODE2.如图,⊙O的直径AB=4,点C在⊙O上,∠ABC=30°,则AC的长是()A.1B.C.D.2【解析】选D.直径所对的圆周角是直角,在直角三角形中,30°的角所对的直角边是斜边的一半.23OABC··3.如图,△ABC的顶点A、B、C都在⊙O上,∠C=30°,AB=2,则⊙O的半径是多少?CABO【解析】连接OA、OB∵∠C=30°,∴∠AOB=60°又∵OA=OB,∴△AOB是等边三角形∴OA=OB=AB=2,即半径为2.·4.求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(提示:作出以这条边为直径的圆)·ABCO求证:△ABC为直角三角形.证明:CO=AB,12以AB为直径作⊙O,∵AO=BO,∴AO=BO=CO.∴点C在⊙O上.又∵AB为直径,∴∠ACB=×180°=90°.1212已知:如图△ABC中,CO为AB边上的中线,且CO=AB∴△ABC为直角三角形.所有顶点都在同一个圆上的多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.如图,四边形ABCD是⊙O的内接四边形,⊙O是四边形ABCD的外接圆.推论4:圆内接四边形的对角互补.例4如图,四边形ABCD内接于⊙O,已知∠BOD=140°,求∠C的度数.解∵四边形ABCD内接于⊙O,∴∠A+∠C=180°.∵∠BOD=140°,∴∠A=∠BOD=×140°=70°.∴∠C=180°-∠A=180°-70°=110°.2121通过本课时的学习,需要我们掌握:1.圆周角定义及其两个特征;2.圆周角定理的内容及其推论;3.思想方法:一种方法和一种思想:在证明中,运用了数学中的分类方法和“化归”思想.分类时应作到不重不漏;化归思想是将复杂的问题转化成一系列的简单问题或已证问题.小结