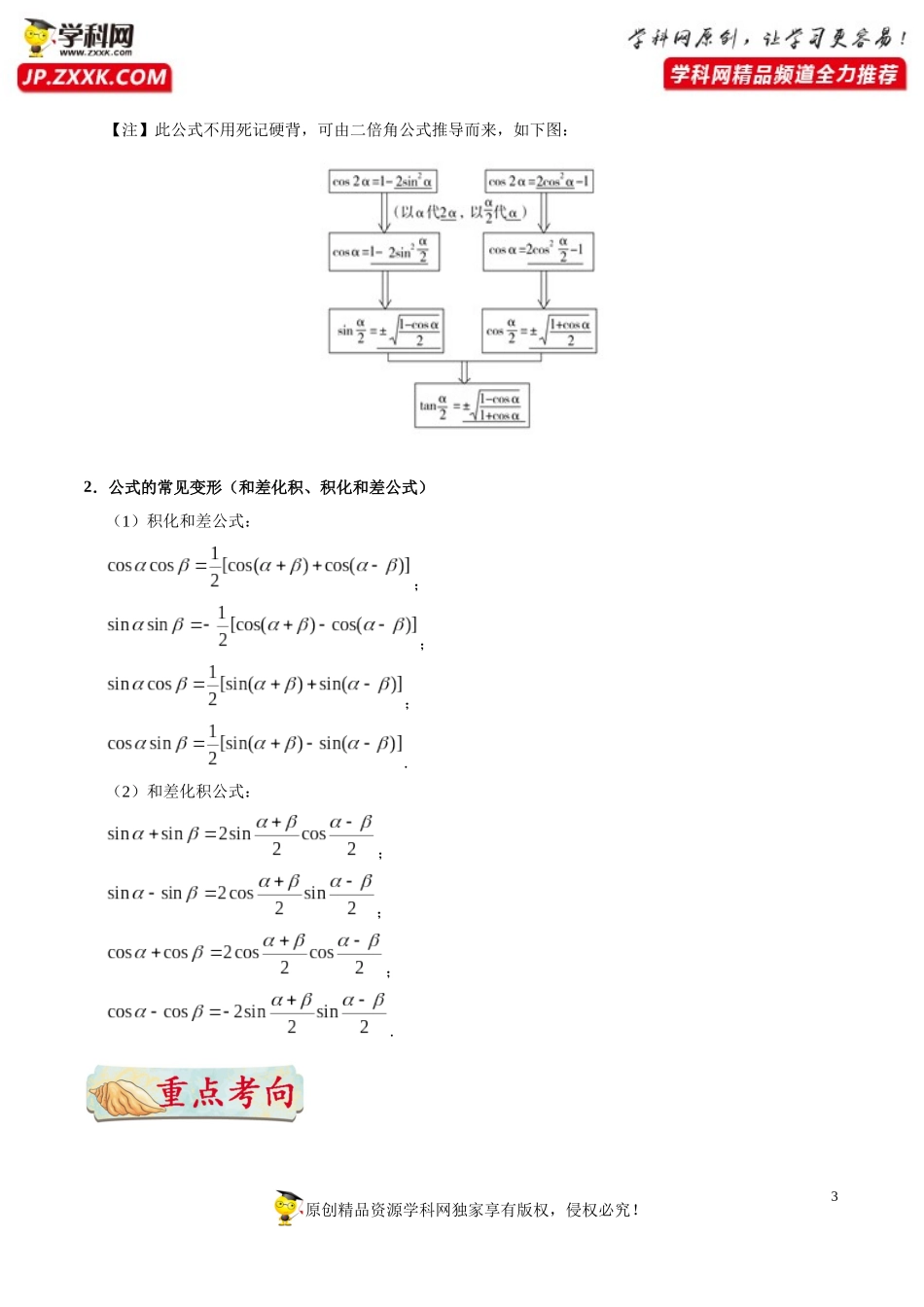
1考点15三角恒等变换三角函数公式,即同角基本关系式、诱导公式以及两角和与差的三角函数公式常结合三角函数性质一起考查,但也要注意单独考查的求值问题,对此,必须首先掌握公式的熟练应用,具体要求如下:1.和与差的三角函数公式(1)会用向量的数量积推导出两角差的余弦公式.(2)能利用两角差的余弦公式导出两角差的正弦、正切公式.(3)能利用两角差的余弦公式导出两角和的正弦、余弦、正切公式,导出二倍角的正弦、余弦、正切公式,了解它们的内在联系.2.简单的三角恒等变换能运用上述公式进行简单的恒等变换(包括导出积化和差、和差化积、半角公式,但对这三组公式不要求记忆).一、两角和与差的三角函数公式1.两角和与差的正弦、余弦、正切公式(1):(2):(3):(4):(5):原创精品资源学科网独家享有版权,侵权必究!2(6):2.二倍角公式(1):(2):(3):3.公式的常用变形(1);(2)降幂公式:;;(3)升幂公式:;;;(4)辅助角公式:,其中,二、简单的三角恒等变换1.半角公式(1);(2);(3).原创精品资源学科网独家享有版权,侵权必究!3【注】此公式不用死记硬背,可由二倍角公式推导而来,如下图:2.公式的常见变形(和差化积、积化和差公式)(1)积化和差公式:;;;.(2)和差化积公式:;;;.原创精品资源学科网独家享有版权,侵权必究!4考向一三角函数式的化简1.化简原则(1)一看角之间的差别与联系,把角进行合理的拆分,正确使用公式;(2)二看函数名称之间的差异,确定使用的公式,常见的有“切化弦”;(3)三看结构特征,找到变形的方向,常见的有“遇到分式要通分”,“遇到根式一般要升幂”等.2.化简要求(1)使三角函数式的项数最少、次数最低、角与函数名称的种类最少;(2)式子中的分母尽量不含根号.3.化简方法(1)切化弦;(2)异名化同名;(3)异角化同角;(4)降幂或升幂.典例1化简:sin(α+β)⋅cosα−12[sin(2α+β)−sinβ].【解析】原式¿sin(α+β)⋅cosα−12⋅2cos(2α+β+β)2sin(2α+β−β2)=sin(α+β)⋅cosα−cos(α+β)sinα=sin(α+β−α)=sinβ【方法技巧】(1)三角化简的常用方法:异名三角函数化为同名三角函数,异角化为同角,异次化为同次,切化弦,特殊值与特殊角的三角函数互化.(2)三角化简的标准:三角函数名称尽量少,次数尽量低,最好不含分母,能求值的尽量求值.(3)在化简时要注意角的取值范围.1.化简求值:原创精品资源学科网独家享有版权,侵权必究!5(1);(2).考向二三角函数的求值问题1.给角求值给角求值中一般所给出的角都是非特殊角,从表面上来看是很难的,但仔细观察会发现非特殊角与特殊角之间总有一定的关系.解题时,要利用观察得到的关系,结合公式将非特殊角的三角函数转化为特殊角的三角函数,从而得解.2.给值求值已知三角函数值,求其他三角函数式的值的一般思路:(1)先化简所求式子.(2)观察已知条件与所求式子之间的联系(从三角函数名及角入手).(3)将已知条件代入所求式子,化简求值.3.给值求角通过求角的某种三角函数值来求角,在选取函数时,有以下原则:(1)已知正切函数值,则选正切函数.(2)已知正、余弦函数值,则选正弦或余弦函数.若角的范围是,则选正、余弦皆可;若角的范围是(0,π),则选余弦较好;若角的范围为,则选正弦较好.4.常见的角的变换(1)已知角表示未知角例如:,,,,,.(2)互余与互补关系原创精品资源学科网独家享有版权,侵权必究!6例如:,.(3)非特殊角转化为特殊角例如:15°=45°−30°,75°=45°+30°.典例2求下列各式的值:(1)cos+cos-2sincos;(2)sin138°-cos12°+sin54°.【解析】(1)cos+cos-2sincos=coscos=2coscoscos=coscos=0.(2)sin138°-cos12°+sin54°=sin42°-cos12°+sin54°=sin42°-sin78°+sin54°=-2cos60°sin18°+sin54°=sin54°-sin18°=2cos36°sin18°=====.【名师点睛】“给角求值”,一般给出的角都是非特殊角,观察发现题中的角与特殊角都有着一定的关系,如和或差为特殊角,必要时运用诱导公式.典例3已知tan(α−β)=,tanβ=,且α,β∈(0...