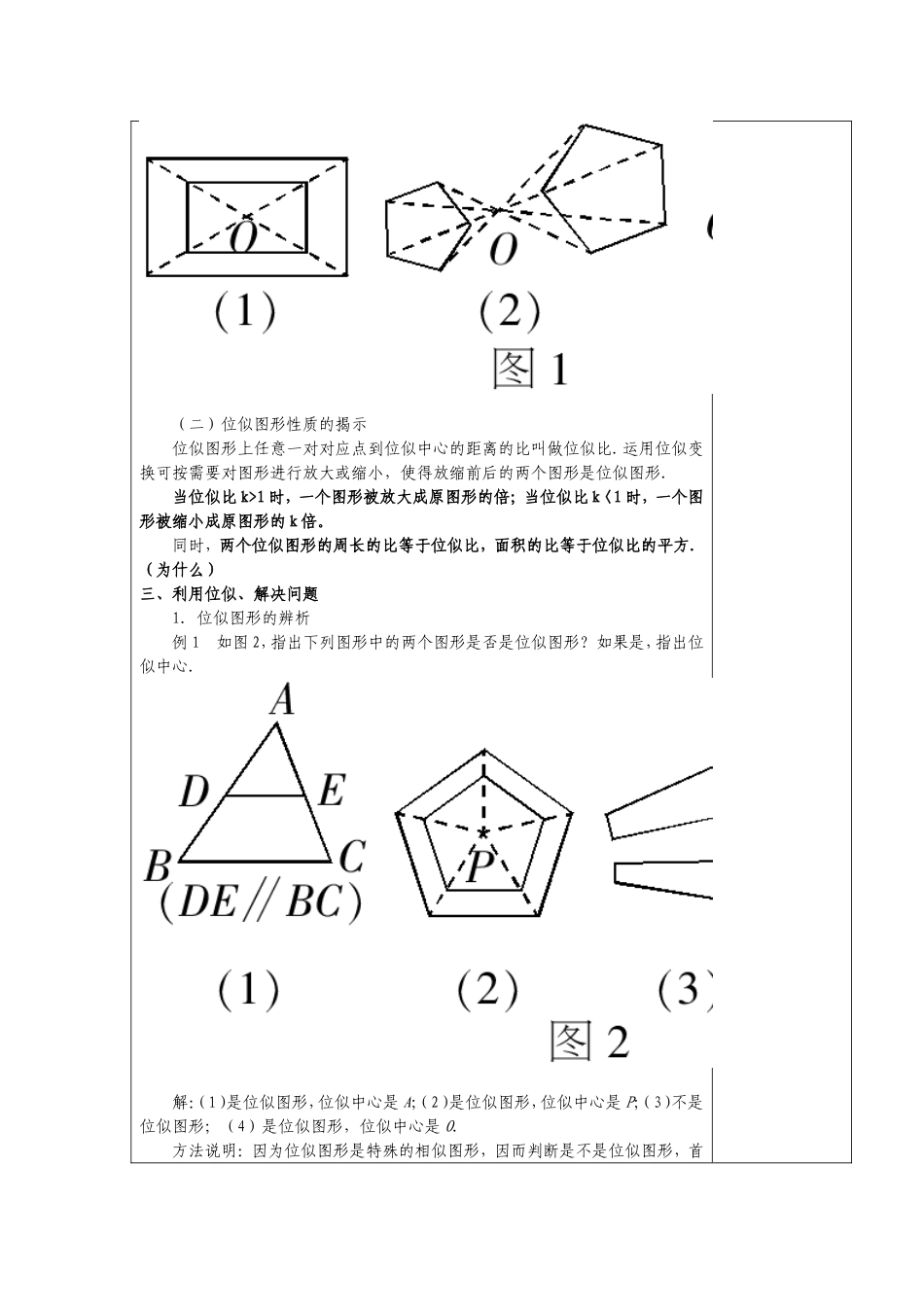
课题位似课型新授教学目标知识与技能经历位似变换、位似的图形抽象得到定义的过程过程与方法掌握位似变换和位似图形的性质情感与态度培养学生独立思考、积极探索的思维品质,善于用数学知识解决身边的数学问题,提高学习数学的热情和积极性.教学重点位似变换的定义和位似图形的性质教学难点位似变换的理解及作图教具准备几何画板教学过程教师活动学生活动一、观察投影,抽象定义1、复习:我们目前为止,学过哪几种图形的变换?经过这几种变换后的图形与原图形之间的关系如何?2、观察:书P95—97,测量并完成P88面的填空3、议一议:P964、抽象:【定义】取定一点O,把图形上任意一点P对应到射线OP(或它的反向延长线)上一点P′,使得线段OP′与OP的比等于常数k(k>0),点O对应到它自身,这种变换叫做位似变换,点O叫作位似中心,常数k叫作位似比,一个图形经过位似变换得到的图形叫作与原图形位似的图形。从位似变换和位似的图形的定义可以得出:两个位似的图形上每一对对应点都与位似中心在一条直线上,并且新图形与原图形上对应点到位似中心的距离之比等于位似比。【思考】两个位似的图形的关系是怎样的呢?如何证明?【结论】两个位似的图形是相似的。二、结合图形、理解定义初次接触位似图形,许多同学往往因位似图形中复杂的线段关系感到它神秘莫测,其实位似图形并不神秘,它实际上是“具有特殊位置关系的两个相似图形”.那么它具有哪些位置关系呢?下面我们一起来探究.(一)位似图形定义的揭示对于位似图形的定义,我们应弄清以下三点:1.位似图形首先是相似图形.2.位似图形都有一个位似中心,它是所有对应点的连线都经过的那个点.两个图形必须同时具备了这两点才是位似图形,缺一不可.3.位似中心的位置由两个位似图形的位置决定,可以在图形的中心、可以在两个图形中间、也可以在两个图形的同一侧,还可以在图形上.如图1所示,图形(1)的位似中心是两个图形的中心,图(2)的位似中心在两个图形之间,图(3)的位似中心在两个图形左侧.(二)位似图形性质的揭示位似图形上任意一对对应点到位似中心的距离的比叫做位似比.运用位似变换可按需要对图形进行放大或缩小,使得放缩前后的两个图形是位似图形.当位似比k>1时,一个图形被放大成原图形的倍;当位似比k〈1时,一个图形被缩小成原图形的k倍。同时,两个位似图形的周长的比等于位似比,面积的比等于位似比的平方.(为什么)三、利用位似、解决问题1.位似图形的辨析例1如图2,指出下列图形中的两个图形是否是位似图形?如果是,指出位似中心.解:(1)是位似图形,位似中心是A;(2)是位似图形,位似中心是P;(3)不是位似图形;(4)是位似图形,位似中心是O.方法说明:因为位似图形是特殊的相似图形,因而判断是不是位似图形,首先看图中的两个图形是否相似,再看对应点的连线是否经过同一个点.2.位似图形的作图例2如图3,已知五边形ABCDE,以点P为位似中心,求作这个五边形的位似图形,使新图形与原图形的位似比为2∶1.解:(1)分别过五边形ABCDE的五个顶点作射线AP、BP、CP、DP、EP;(2)在这些射线上依次截取PA1=2PA,PB1=2PB;PC1=2PC,PD1=2PD,PE1=2PE;(3)顺次连结A1,B1,C1,D1,E1,所得图形就是符合要求的图形.方法说明:根据位似图形中的一个图形和位似中心、位似比求作另一个图形,其根据就是“位似图形上任意一对对应点到位似中心的距离的比等于位似比”,而具体做法则是先根据位似比找出另一个图形的关键点,然后再按一定的顺序连结这些点即可.3.位似图形的应用例3一般在室外放映的电影胶片上每一个图片的规格为:3.5cm×3.5cm,放映屏幕的规格为2m×2m,若放映机的光源距胶片20cm,问屏幕应在离光源多远的地方,放映的图像刚好布满整个屏幕?分析:胶片上的图形和银屏上的图形是位似图形,光源是位似中心,则可运用位似图形的知识来解答.解:如图4所示,根据已知数据可知,位似比.设屏幕距离光源xcm,根据位似图形的性质,可得,所以.答:屏幕应在离光源的地方,放映的图像刚好布满整个屏幕.方法说明:在利用位似图形解决实际问题时,首先要将其抽象为位似模型...