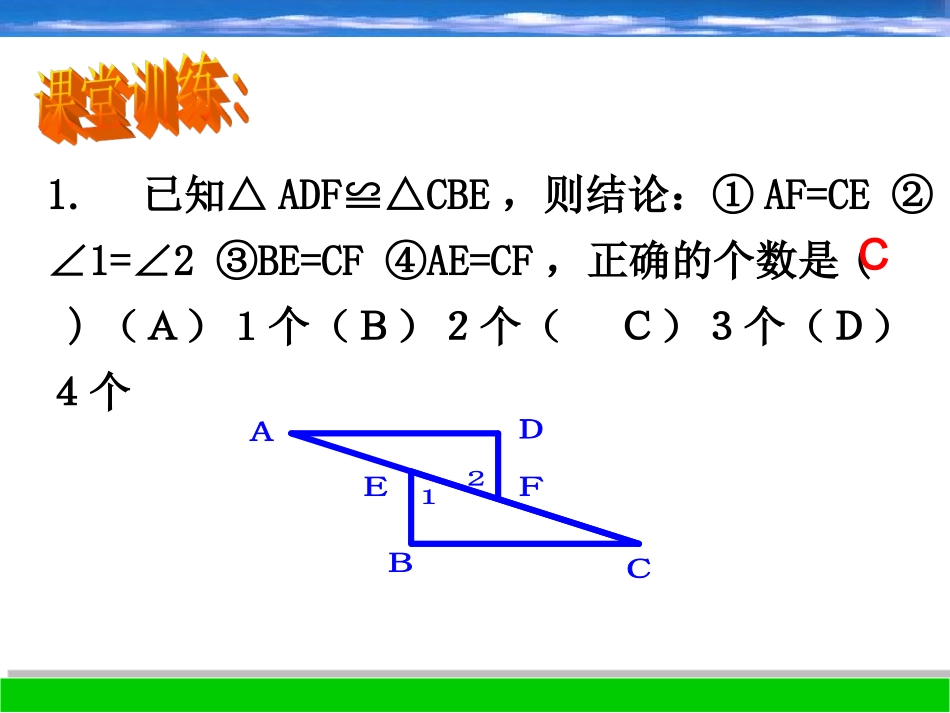
1.5三角形全等的判定(1)1.5三角形全等的判定(1)1.已知△ADF≌△CBE,则结论:①AF=CE②∠1=∠2③BE=CF④AE=CF,正确的个数是()(A)1个(B)2个(C)3个(D)4个21FCDEBAC用刻度尺和圆规画△ABC使其三边的长为AB=6cm,AC=4cm,BC=3cm。画法:1.画线段AB=6cm2.分别以A,B为圆心,4cm,3cm为半径画弧交于点C(C′)3.连接AC,BC.∴△ABC即为所求的三角形把你画的三角形与其他同学所画的三角形进行比较,它们能互相重合吗?在△ABC与△DEF中,∴△ABCDEF()≌△AB=DEAC=DFBC=EF三边对应相等的两个三角形全等.(简写成“边边边”或“SSS”)SSSABC〃\≡DEF〃\≡知识点一:AABBCCDD如图,在四边形如图,在四边形ABCDABCD中中,AB=CD,AB=CD,,AD=BCAD=BC,,则则∠A=C,∠请说明理由。解:解:在在ABDABD和和CDBCDB中中AB=CDAB=CD(已知)(已知)AD=BCAD=BC(已知)(已知)BD=DBBD=DB(())()∴ABDABD≌CDBCDB∴∠A=∠C()全等三角形的对应角相等全等三角形的对应角相等公共边公共边SSS小结:欲证角相等,转化为证三角形全等。1:1:如图,点如图,点B,E,C,FB,E,C,F在同一直线上在同一直线上,,且且AB=DAB=DE,AC=DF,BE=CF,E,AC=DF,BE=CF,试说明试说明△ABCDEF.≌△ABECFD解:BE=CF()∵∴BE+EC=CF+EC,即BC=EF在⊿ABC和⊿DEF中AB=___()____=DF()BC=___∴△ABCDEF()≌△已知DEDE已知ACAC已知EFSSS2:2:如图,已知如图,已知AB=DE,BC=EF,AF=DC,AB=DE,BC=EF,AF=DC,试说明试说明∠EFD=BCA∠.ABECFD知识点二:已知∠BAC,用直尺和圆规作∠BAC的角平分线AD.BAC直尺是指使用的尺只能用于画直线,不能用来量长度2:如图,已知AB=AC,AD=AE,BD=CE,则图中全等的三角形有_______对,分别把它们表示出来.ABCDE23:3:如图,点如图,点CC是是ABAB的中点的中点,AD=CE,CD=BE,,AD=CE,CD=BE,B=∠58°,,A=72∠°,求∠DCE.ABCDE4.如图△ABC是一个钢架,AB=AC,AD是连结点A和BC中点的支架,求证:ADBC⊥证明:在△ABD和△ACD中,AB=AC(已知)AD=AD(公用边)DB=DC(已知)∴△ABDACD≌△(SSS)∴∠1=2(∠全等三角形对应角相等)∴∠1=21∠BDC=900(平角定义)∴ADBC⊥(垂直定义)ABCD211.边边边公理:有三边对应相等的两个三角形全等简写成“边边边”(SSS)2.证明线段(或角相等)转化1.说明两个三角形全等所需的条件应按对应边的顺序书写.2.结论中所出现的边必须在所证明的两个三角形中.用结论说明两个三角形全等需注意证明线段(或角)所在的两个三角形全等.3.四边形问题转化为三角形问题来解决。1:如图中,AB=CD,若添加________条件,可根据________判定△ABCCDA≌△ABCDBC=DASSS2:如图中,已知AB=AC,D是BC上的一点,要想使△ABDACD,≌△则需添加的一个条件为__________________.ABCDBD=DC或D是BC的中点②∵______________∴∠A=C∠()在△ADE与△CBF中解:①∵E、F分别是AB,CD的中点()又∵AB=CD∴AE=CF∴△ADECBF≌△()AE=______=______=___∴AE=ABCF=CD()1212如图,已知AB=CD,AD=CB,E、F分别是AB,CD的中点,且DE=BF,说出下列判断成立的理由.①△ADECBF≌△②∠A=C∠线段中点的定义CFADABCDSSS△ADECBF≌△全等三角形对应角相等已知ADBCFECB如图中,AB=AC,BD=CD,你能判断∠B=C∠吗?BACD注意:为了解题需要,要在原图形上添一些线,这些线叫做辅助线,辅助线通常画成虚线。如图,已知AB=CD,AD=CB,求证:∠B=∠D证明:连结AC,∴△ABCCDA≌△(SSS)∴∠B=∠D(全等三角形对应角相等)问:1.此题添加辅助线,若连结BD行吗?2.在原有条件下,还能推出什么结论?ABCDABCDAB=CD(已知)AC=AC(公用边)BC=AD(已知)在△ABC和△ADC中,小结:四边形问题转化为三角形问题解决。