直角三角形的性质和判定 (2)VIP免费

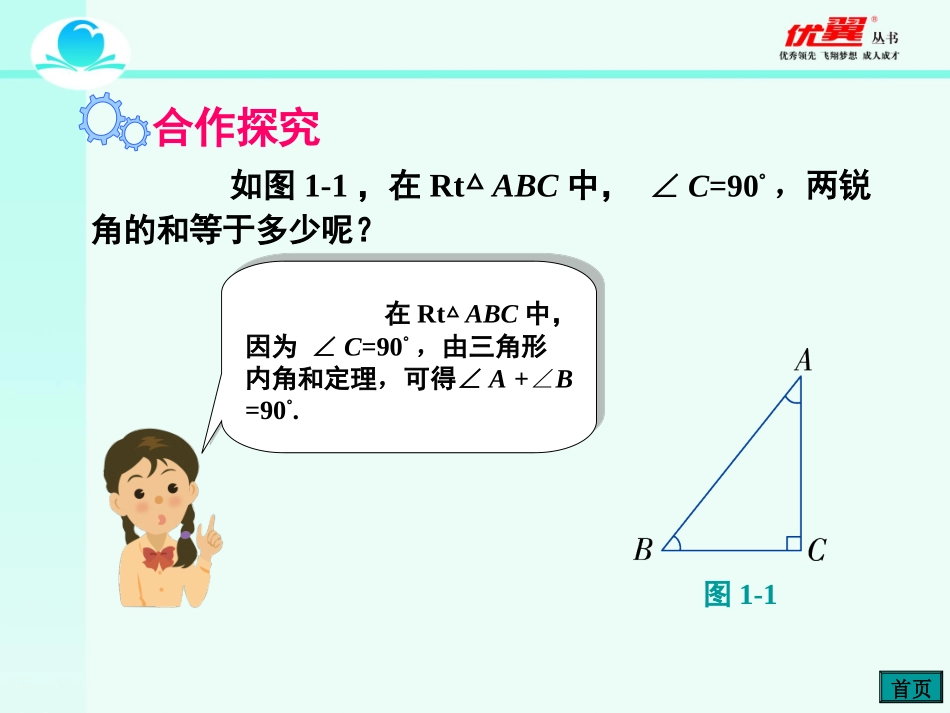
1.11.1直角三角形的性质和判定直角三角形的性质和判定（（ⅠⅠ））复习引入合作探究课堂小结随堂训练第第11课时直角三角形的性质和判定课时直角三角形的性质和判定第第11章章直角三角形直角三角形三角形顶点与对边中点的连线段1.直角三角形的定义2.三角形内角和的性质有一个是直角的三角形叫直角三角形三角形内角和等于180°3.三角形中线的定义这节课我们一起探索直角三角形的判定与性质复习引入首页如图1-1，在Rt△ABC中，∠C=90°，两锐角的和等于多少呢？图1-1在Rt△ABC中，因为∠C=90°，由三角形内角和定理，可得∠A+∠B=90°.在Rt△ABC中，因为∠C=90°，由三角形内角和定理，可得∠A+∠B=90°.合作探究首页结论直角三角形的两个锐角互余.直角三角形的两个锐角互余.由此得到：议一议议一议议一议议一议议一议议一议有两个锐角互余的三角形是直角三角形吗？如图1-2，在△ABC中，∠A+∠B=90°，那么△ABC是直角三角形吗？在△ABC中，因为∠A+∠B+∠C=180°，又∠A+∠B=90°，所以∠C=90°.于是△ABC是直角三角形.在△ABC中，因为∠A+∠B+∠C=180°，又∠A+∠B=90°，所以∠C=90°.于是△ABC是直角三角形.图1-2结论有两个角互余的三角形是直角三角形.有两个角互余的三角形是直角三角形.由此得到：如图1-3，画一个Rt△ABC，并作出斜边AB上的中线CD，比较线段CD与线段AB之间的数量关系，你能得出什么结论？图1-3我测量后发现CD=AB.我测量后发现CD=AB.12线段CD比线段AB短.线段CD比线段AB短.图1-3是否对于任意一个Rt△ABC，都有CD=成立呢？12AB图1-4如图1-3，如果中线CD=AB，则有∠DCA=∠A.由此受到启发，在图1-4的Rt△ABC中，过直角顶点C作射线交AB于，使，12CD=ADD∠=∠ADCA则.CD图1-3∠A+∠B=90°，又∵90DCA+DCB，∴BDCB.CD=BD.∴故得12CD=AD=BD=AB.D∴点是斜边上的中点，即是斜边的中线.ABCDCD从而CD与重合，且CDAB.12图1-4结论直角三角形斜边上的中线等于斜边的一半.直角三角形斜边上的中线等于斜边的一半.由此得到：举例例1已知：如图1-5，CD是△ABC的AB边上的中线，且.求证：△ABC是直角三角形.12CDAB图1-5证明：因为，所以∠1=∠A，(等边对等角)∠2=∠B.12CDAB=BD=AD图1-5根据三角形内角和性质，有∠A+∠B+∠ACB=180°，即得∠A+∠B+∠1+∠2=180°，2(∠A+∠B)=180°.所以∠A+∠B=90°.根据直角三角形判定定理，所以△ABC是直角三角形.1.在Rt△ABC中，斜边上的中线CD=2.5cm，则斜边AB的长是多少？解解AB=2CD=2×2.5=5(cm).随堂训练首页2.如图，AB∥CD，∠BAC和∠ACD的平分线相交于H点，E为AC的中点，EH=2.那么△AHC是直角三角形吗？为什么？若是，求出AC的长.解因为AB∥CD，所以∠BAC+∠DCA=180°.又，，所以所以△AHC是直角三角形.在Rt△AHC中，EH为斜边上的中线，所以有，由EH=2易知AC=4.12CAHBAC12ACHDCA1902CAH+ACHBAC+DCA=()12EHAC3.如图所示，在锐角三角形ABC中，CD，BE分别是AB，AC边上的高，且CD，BE交于一点P，若∠A=50°，则∠BPC的度数是（）.A.150°B.130°C.120°D.100°因为BE，CD是ABC的高，所以∠BDP=90°，∠BEA=90°.又∠A=50°，所以∠ABE=90°-∠A=90°-50°=40°.所以∠BPC=∠ABE+∠BDP=90°+40°=130°.故应选择B.解BABCDO4.如图，AB⊥DB,CD⊥DB,下列说法错误的是（）A.一定有∠A=∠CB.只要有一边相等就有△ABO≌△CDOC.只要再给一个条件就能得到△ABO≌△CDOD.有OA=OC或OB=OD,就有AB=CDCABCD5.如图，AB=AC,AD⊥BC.求证：BD=CD.1.直角三角形的判定定理和性质定理；2.应用定理进行推理论证解决有关问题.课堂小结首页课后作业见《学练优》本课“课后巩固提升”