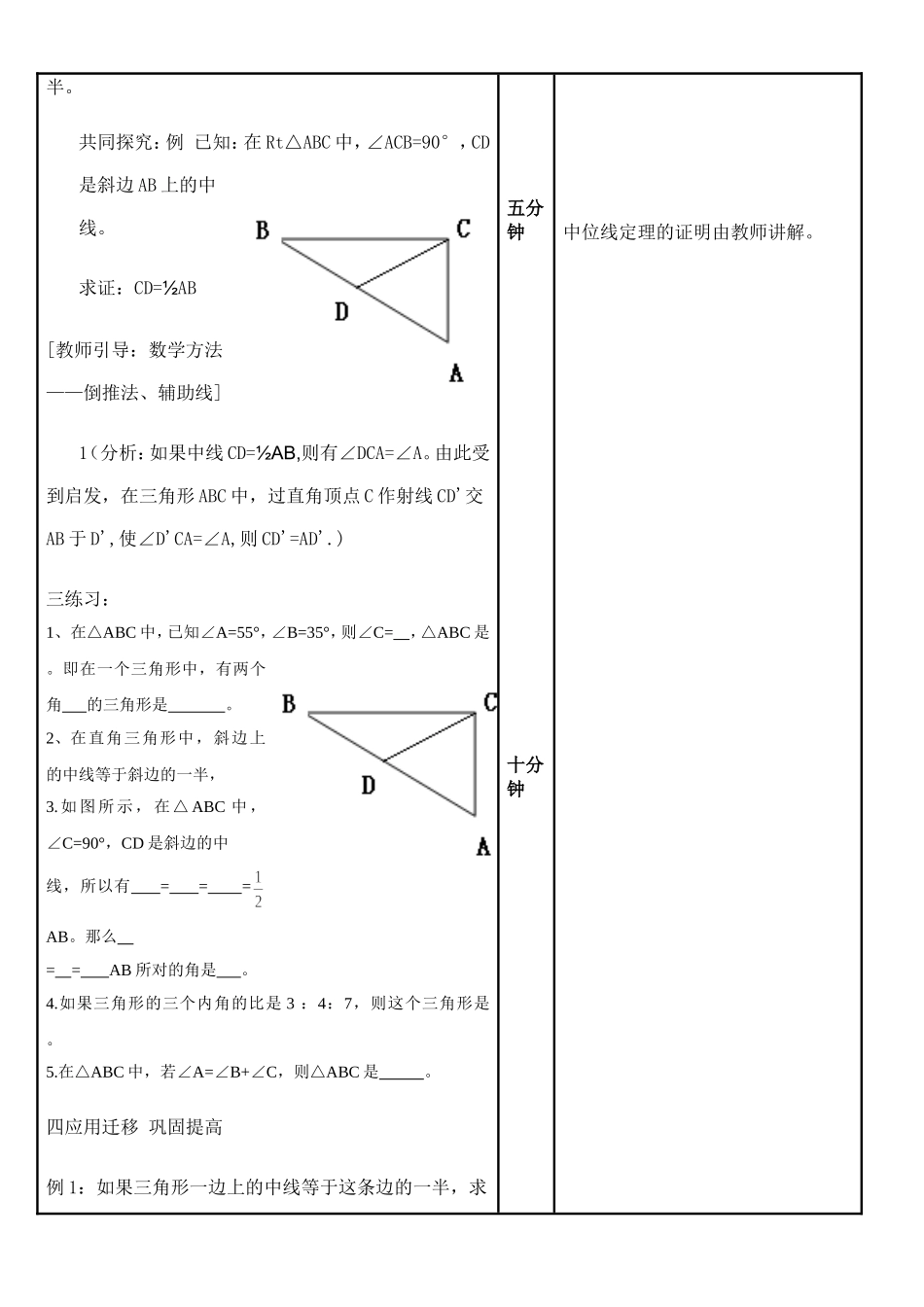
禾青中心学校教学设计科目:数学年级:八年级主备人:周仁审核人:周仁时间:课题直角三角形的性质和判定(1)共1课时第1课时学习目标知识与技能:1理解并掌握直角三角形的判定定理和斜边上的中线性质定理2能应用直角三角形的判定与性质,解决有关问题。情感、态度与价值观:感受数学活动中的多向思维、合作交流的价值,主动参与数学思维与交流活动。重点难点理解与掌握直角三角形的判定定理和斜边上中线性质定理(难点)能应用直角三角形的判定和性质,解决有关问题。(重点)学习内容时间分配五分钟十五分钟学习方法一、情景导入,生成问题。有三个村庄,位于一个直角三角形的三个顶点,现要建一个垃圾中转站,使它到三个村庄的距离相等,请问,垃圾中转站应建在什么位置?教学引入1、三角形的内角和是多少度。学生回答。2、什么是直角三角形?日常生活中有哪些物品与直角三角形有关?请举例说明。3、等腰三角形有哪些性质?二、探究新知1、探究直角三角形判定定理:⑴观察小黑板上的三角形,从∠A+∠B的度数,能说明什么?——两个锐角互余的三角形是直角三角形。⑵讨论:直角三角形的性质和判定定理是什么关系?2、探究直角三角形性质定理:⑴学生画出直角三角形ABC斜边的中线CD。⑵测量并讨论斜边上的中线的长度与斜边的关系。⑶学生猜想:直角三角形中斜边上的中线等于斜边的一由生活实际问题入手,引入课题,激起学生兴趣。以学生为主体,学生自主探究,得出结论半。共同探究:例已知:在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线。求证:CD=½AB[教师引导:数学方法——倒推法、辅助线]1(分析:如果中线CD=½AB,则有∠DCA=∠A。由此受到启发,在三角形ABC中,过直角顶点C作射线CD'交AB于D',使∠D'CA=∠A,则CD'=AD'.)三练习:1、在△ABC中,已知∠A=55°,∠B=35°,则∠C=,△ABC是。即在一个三角形中,有两个角的三角形是。2、在直角三角形中,斜边上的中线等于斜边的一半,3.如图所示,在△ABC中,∠C=90°,CD是斜边的中线,所以有===AB。那么==AB所对的角是。4.如果三角形的三个内角的比是3:4:7,则这个三角形是。5.在△ABC中,若∠A=∠B+∠C,则△ABC是。四应用迁移巩固提高例1:如果三角形一边上的中线等于这条边的一半,求五分钟十分钟中位线定理的证明由教师讲解。证,这个三角形是直角三角形。已知:如图CD是三角形ABC的AB边上的中线,CD=½AB。求证:三角形ABC是直角三角形。提示:倒推法,要证明ABC是直角三角形,只有通过定义和判定定理,定义与判定定理都与角有关系。现在我们只有边的关系,我们学过的边与角能联系起来的就是等腰三角形。还要找到与90°有关的角,但是我们只知道三角形的内角和为180°。通过提示,请同学们自己写出证明过程。补充例题如图,AB∥CD,∠BAC和∠ACD的平分线相交于H点,E为AC的中点,EH=2,求AC的长。五、课堂小结:1、两个锐角互余的三角形是直角三角形。2、在直角三角形中,斜边上的中线等于斜边的一半。反过来讲也正确。六、作业布置P7练习题五分钟五分钟教学反思: