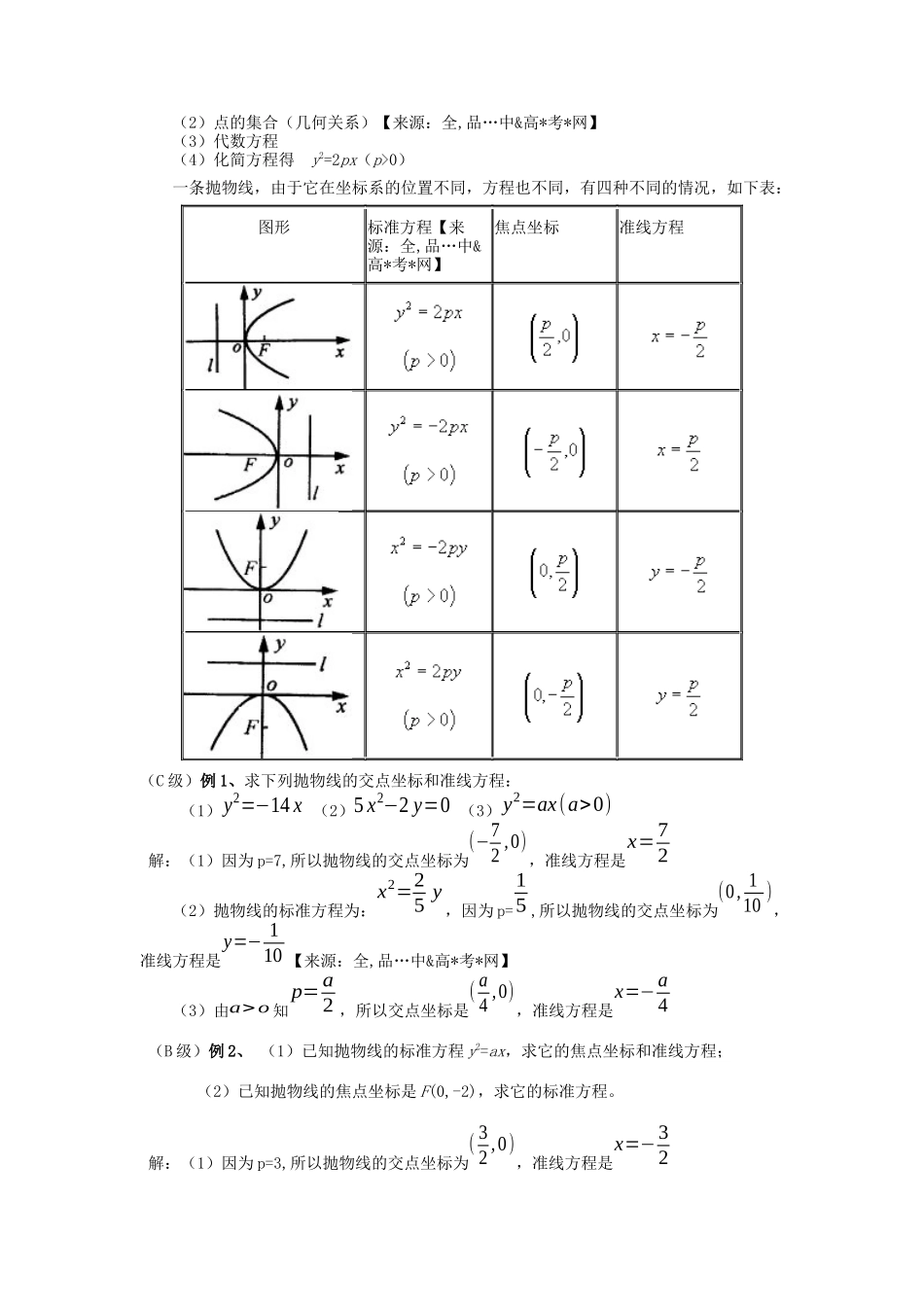
一、教材分析:抛物线是学生通过学习函数知识而熟悉的曲线,本节课利用解析法研究抛物线的方程及其性质,可以使学生扩展过去对抛物线的认识,并在以后将三种圆锥曲线的定义统一起来。通过本节课的学习,使学生进一步掌握求曲线方程的方法。按照相应的教学参考书的要求,应共讲四课时,本节为第一课时,主要内容是推导抛物线的四种标准方程。课本是先用作图的方法画出了开口向右的图形,然后旋转成开口向上的图形,让学生从图形上认可该曲线为抛物线,从而给出抛物线的定义,然后推导了形如y2=2px(p>0)的标准方程。二、学情分析:1.学生在代数运算方面欠缺,所以要进一步理解并掌握代数法在解析几何中的作用,提高学生解方程组的计算能力,通过“数”研究“形”。2、学生计算带有绝对值号和根号的式子时都不知所措,导致公式推导存在问题,老师应该在这边方面予以正确引导。三、教学目标:1、通过探究曲线的方程与类型,经历数学化的过程,从而使学生理解并掌握抛物线的定义及标准方程和图形。学生体会到数学的简洁美、和谐美,培养精益求精的治学态度和勇于探索的精神。2、通过习题的演练,使学生能根据抛物线的标准方程求出其焦点、和准线方程,并能根据其性质画出抛物线的图形。养成学生会初步利用待定系数法求抛物线的标准方程的解题思维。培养学生观察、发现问题和解决问题的能力,进一步理解掌握圆锥曲线。四、教学重点、难点:重点:掌握抛物线的定义、焦点、准线的概念;能根据条件求抛物线的方程。难点:建立适合的坐标系求抛物线的方程,由方程求焦点和准线方程。五、教学过程(一)复习提问、导入课题[教师提问]:1、椭圆与双曲线的定义?(引导学生配方,并回答。)教师引出,与一个定点的距离和一条定直线的距离的比是常数e的点的轨迹,当01时是双曲线,那么当e=1时是什么曲线呢?这就是今天我们要学习的第三种圆锥曲线—抛物线,以及它的定义和标准方程.(二)新课讲授1.抛物线的定义平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线.点F叫做抛物线的焦点,定直线l叫做抛物线的准线.2.抛物线的标准方程设定点F到定直线l的距离为p(p>0).【来源:全,品…中&高*考*网】(1)建系设点(2)点的集合(几何关系)【来源:全,品…中&高*考*网】(3)代数方程(4)化简方程得y2=2px(p>0)一条抛物线,由于它在坐标系的位置不同,方程也不同,有四种不同的情况,如下表:图形标准方程【来源:全,品…中&高*考*网】焦点坐标准线方程(C级)例1、求下列抛物线的交点坐标和准线方程:(1)y2=−14x(2)5x2−2y=0(3)y2=ax(a>0)解:(1)因为p=7,所以抛物线的交点坐标为(−72,0),准线方程是x=72(2)抛物线的标准方程为:x2=25y,因为p=15,所以抛物线的交点坐标为(0,110),准线方程是y=−110【来源:全,品…中&高*考*网】(3)由a>o知p=a2,所以交点坐标是(a4,0),准线方程是x=−a4(B级)例2、(1)已知抛物线的标准方程y2=ax,求它的焦点坐标和准线方程;(2)已知抛物线的焦点坐标是F(0,-2),求它的标准方程。解:(1)因为p=3,所以抛物线的交点坐标为(32,0),准线方程是x=−32(2)因为抛物线的焦点在Y轴负半轴上,且p2=2,p=4所以,所求抛物线的标准方程为:x2=−8y六、课时小结:1.抛物线的定义及焦点、准线的概念。2.如何根据条件求抛物线方程。七、课时作业:(C级)1、抛物线的焦点是(−14,0),则准线方程为(D)A、x2=−yB、x2=yC、y2=xD、y2=−x(C级)2、y2=8x的准线方程是y=−132(C级)3、抛物线y=14x2的焦点坐标是(C)A、(0,116)B、(116,0)C、(0,1)D、(0,1)(B级)4、抛物线y2=4x上一点p(x0,y0)到焦点F的距离为4,则P点的坐标是(3,2√3)或(3,−2√3)(A级)5、若抛物线y2=2x上两点AB到焦点的距离之和为5,则线段AB的中点横坐标是2八、板书设计抛物线及其标准方程1.抛物线的定义2.抛物线的标准方程设定点F到定直线l的距离为p(p>0).(1)建系设点(2)点的集合(几何关系)(3)代数方程(4)化简方程得y2=2px(p>0)3.抛物线的方程:y2=−2px(p>0)、y2=2px(p>0)x2=2py(p>0)x2=−2py(p>0)例1【来源:全,品…中&高*考*网】例2