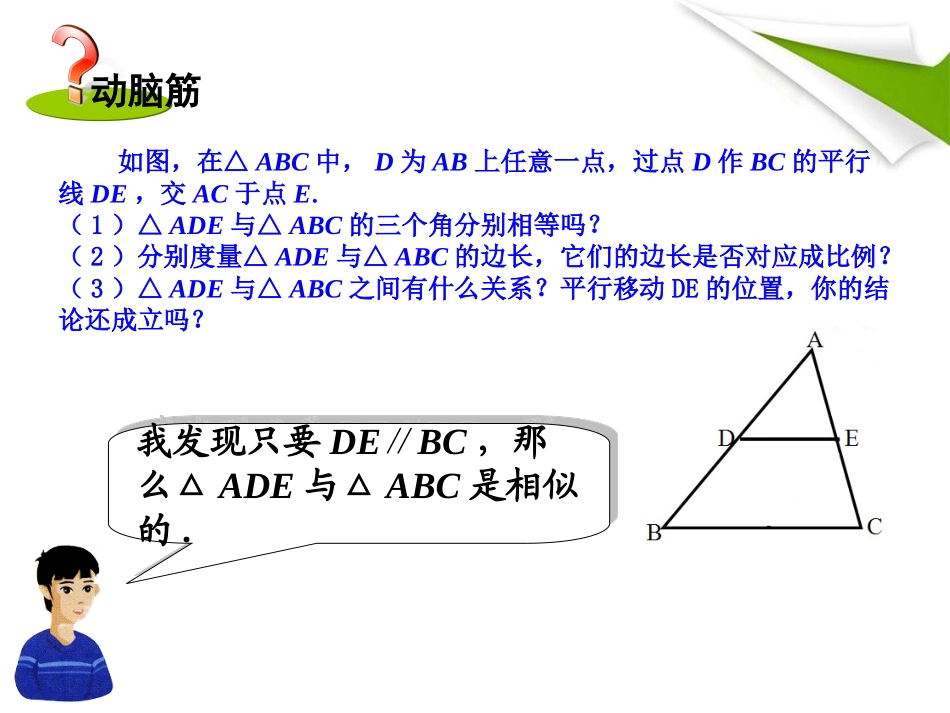
3.4.1相似三角形的判定第1课时相似三角形判定的基本定理探究在八年级上册,我们已经探讨了两个三角形全等的条件,下面我们来探讨两个三角形相似的条件.为了研究满足什么条件的两个三角形相似,我们先来探究下述问题.动脑筋如图,在△ABC中,D为AB上任意一点,过点D作BC的平行线DE,交AC于点E.(1)△ADE与△ABC的三个角分别相等吗?(2)分别度量△ADE与△ABC的边长,它们的边长是否对应成比例?(3)△ADE与△ABC之间有什么关系?平行移动DE的位置,你的结论还成立吗?我发现只要DE∥BC,那么△ADE与△ABC是相似的.我发现只要DE∥BC,那么△ADE与△ABC是相似的.下面我们来证明:在△ADE与△ABC中,∠A=∠A.∵DEBC∥,∴∠ADE=∠B,∠AED=∠C.∵DEBC∥,DFAC∥,如图,过点D作DFAC∥,交BC于点F.∴,.ADAEADCFABACABCB∵四边形DFCE为平行四边形,∴DE=FC.∴.ADAEDEABACBC∴△ADE∽△ABC结论由此得到如下结论:平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似.例题例题例1如图,在△ABC中,已知D,E分别是AB,AC边的中点.求证:△ADE∽△ABC.证明∵点D,E分别是AB,AC边的中点,∴DE∥BC.∴△ADE∽△ABC.例题例题例2如图,点D为△ABC的边AB的中点,过点D作DE∥BC,交边AC于点E.延长DE至点F,使DE=EF.求证:△CFE∽△ABC.证明∵DE∥BC,点D为△ABC的边AB的中点,∴AE=CE.∴△ADE∽△ABC.又DE=FE,∠AED=∠CEF,∴△ADE≌△CEF.∵DE∥BC,∴△CFE∽△ABC.跟踪练习跟踪练习1.如图,在Rt△ABC中,∠C=90°.正方形EFCD的三个顶点E,F,D分别在边AB,BC,AC上.已知AC=7.5,BC=5,求正方形的边长.解:∵四边形EFCD是正方形,∴EDBC,ED=DC=FC=EF.∥AEDABC.ADEDACBC=.7.57.55ACDCEDDCDCACBC=,即=.3DE,即正方形的边长为3.跟踪练习跟踪练习2.如图,已知点O在四边形ABCD的对角线AC上,OE∥BC,OF∥CD.试判断四边形AEOF与四边形ABCD是否相似,并说明理由.解:∵OE∥BC,OF∥CD,∴∠AEO=ABC,AOE=ACB,AOF=ACD,AFO∠∠∠∠∠∠=ADC.∠∴∠AOE+AOF=ACB+ACD,∠∠∠即∠EOF=BCD.∠又∵OE∥BC,OF∥CD,∴△AOE~ACB,AOF~ACD.△△AEEDAOOFADABBCACCDDC====.∴四边形AEOF与四边形ABCD相似.