一元二次方程根与系数的关系 (2)VIP免费

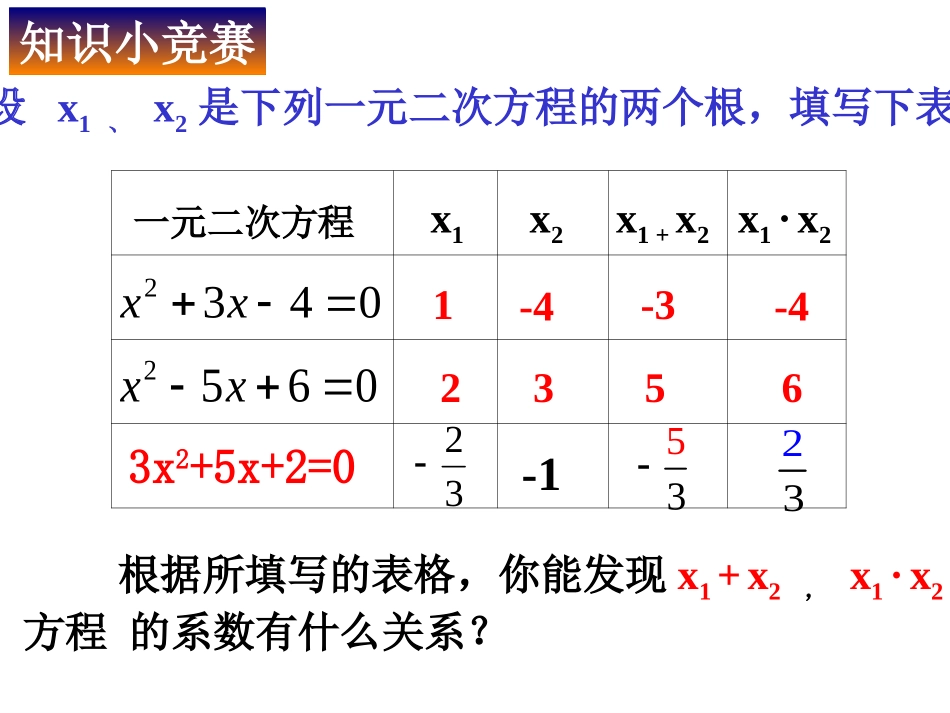
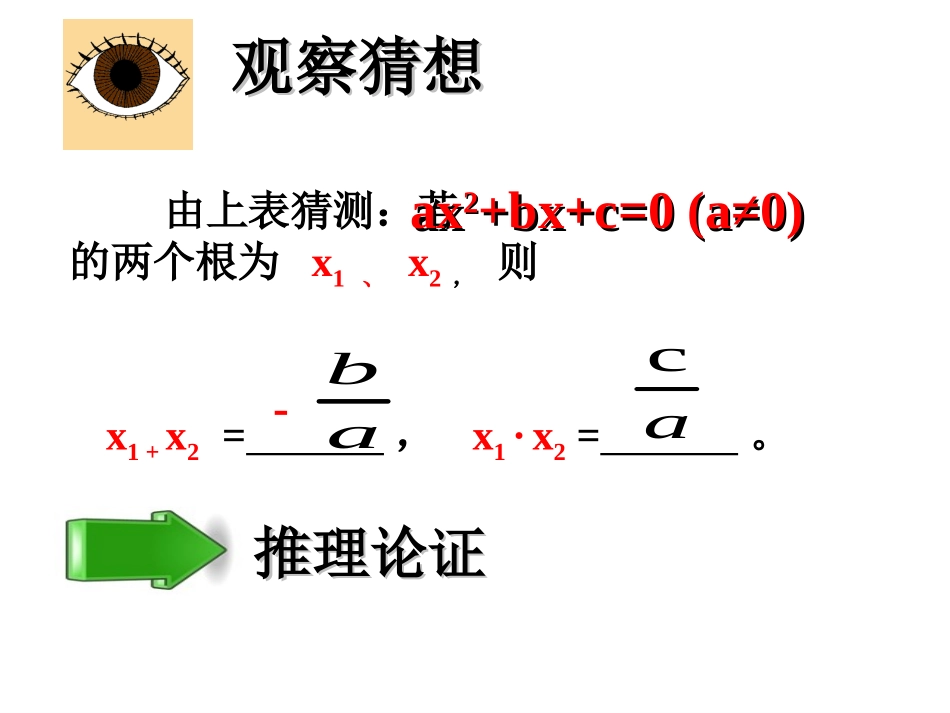
知识小竞赛设x1、x2是下列一元二次方程的两个根，填写下表x1·x2x1+x20652xx0432xx一元二次方程根据所填写的表格，你能发现x1+x2，x1·x2方程的系数有什么关系？x1x21-4-3-423563x2+5x+2=03523-132由上表猜测：若的两个根为x1、x2，则axax22+bx+c=0(a≠0)+bx+c=0(a≠0)x1·x2=。x1+x2=，ab-ac观察猜想观察猜想推理论证推理论证ababaacbbaacbbxx2224242221acaacbbaacbbaacbbxx2222222144)24()24(212,0,0xxacbxax的两个根是如果一元二次方程的根与系数的关系：如果方程ax2+bx+c=0(a≠0)的两个根是x1,x2,那么x1+x2=,x1x2=注：能用公式的前提条件为△=b2-4ac≥0在使用根与系数的关系时，应注意：⑴不是一般式的要先化成一般式；⑵在使用X1+X2=时，注意“－”不要漏写。ab-acab-如果方程x2+px+q=0的两根是X1，X2，那么X1+X2=,X1X2=.－Pq一元二次方程根与系数的关系是法国数学家“韦达”发现的,所以我们又称之为韦达定理.1．（口答）下列方程中，两根的和与两根的积各是多少？（1）（2）（3）（4）（5）（6）练一练练一练··例1、已知方程x2-(k+1)x+3k=0的一个根是2,求它的另一个根及k的值.解法一：设方程的另一个根为x2.由根与系数的关系，得2＋x2=k+12x2=3k解这方程组，得x2=－3k=－2答：方程的另一个根是－3,k的值是－2.例1、已知方程x2-(k+1)x+3k=0的一个根是2,求它的另一个根及k的值。解法二：设方程的另一个根为x2.把x=2代入方程，得4-2(k+1)+3k=0解这方程，得k=-2由根与系数的关系，得2x2＝3k即2x2＝－6∴x2＝－3答：方程的另一个根是－3,k的值是－2.例2、方程2x2-3x+1=0的两根记作x1,x2，不解方程，求：（1）;（2);•;(4).2221xx2111xx)1)(1(21xx21xx另外几种常见的求值:2111.1xx2121xxxx)1)(1.(321xx1)(2121xxxx1221.2xxxx212221xxxx21212212)(xxxxxx21.4xx221)(xx212214)(xxxx1、已知方程3x2－19x+m=0的一个根是1，求它的另一个根及m的值。2、设x1,x2是方程2x2＋4x－3=0的两个根，求(x1+1)(x2+1)的值.212xx21xx41141221xx2221xx221)(xx＝221)(xx221)(xx214xx＝求与方程的根有关的代数式的值时,一般先将所求的代数式化成含两根之和,两根之积的形式,再整体代入.4.已知方程的两个实数根是且，求k的值.解：由根与系数的关系得x1+x2=-k，x1x2=k+2又x12+x22=4即(x1+x2)2-2x1x2=4K2-2(k+2）=4K2-2k-8=0∵△=K2-4k-8当k=4时，△=-8＜0∴k=4(舍去）当k=-2时，△=4＞0∴k=-2解得：k=4或k=－2022kkxx2,1xx42221xx6.已知关于x的方程x2+(2m-1)x+m2=0有两个实数根x1、x2.（1）求实数m的取值范围；（2）当x12-x22=0时，求m的值.7.（2013•荆州）已知：关于x的方程kx2－(3k－1)x+2(k－1)=0（1）求证：无论k为何实数，方程总有实数根；（2）若此方程有两个实数根x1，x2,且│x1－x2│=2,求k的值.2、熟练掌握根与系数的关系；3、灵活运用根与系数关系解决问题.1.一元二次方程根与系数的关系？acabaCbxaxxxxxxx2121212.;,)0(0则有的两根分别是如果小结：8、已知关于X的方程mx2-(2m-1)x+m-2=0(m﹥0)(1)此方程有实数根吗？（2）如果这个方程的两个实数根分别为x1，x2，且（x1-3)(x2-3)=５m，求m的值。