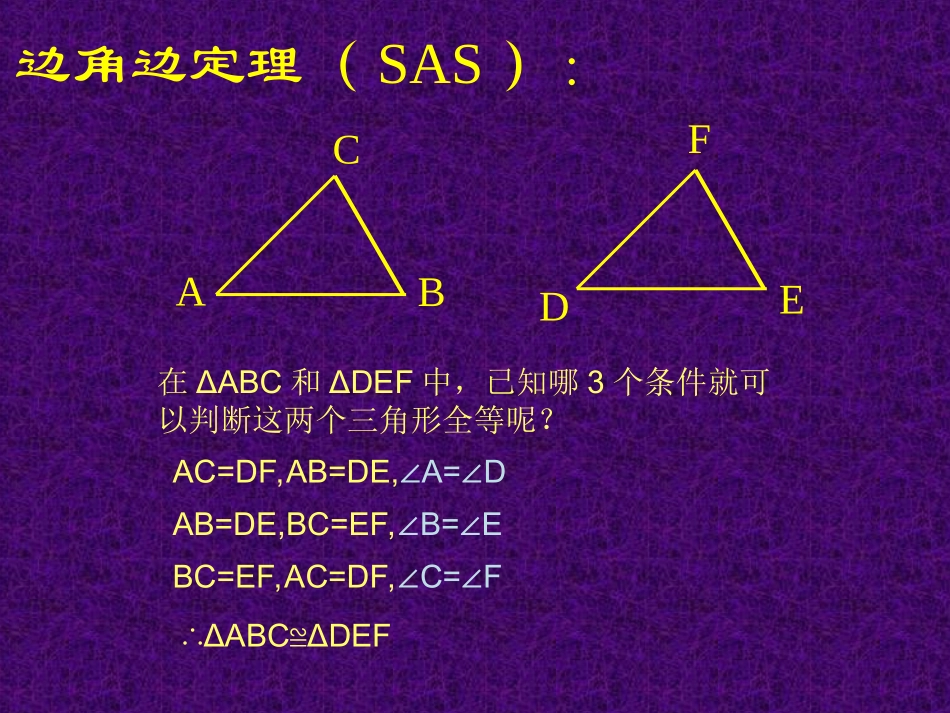
三角形全等的判定(1)――边角边定理(SAS)之前要求画ΔABC,(使得∠A=45°,AB=4cm,AC=3cm,)画好后与其他同学比较发现,画出来的三角形是全等的。只要确定一个三角形的两边及其夹角,那么这个三角形的形状就确定下来了。ACDEF边角边定理(SAS):B在ΔABC和ΔDEF中,已知哪3个条件就可以判断这两个三角形全等呢?AC=DF,AB=DE,A=D∠∠AB=DE,BC=EF,B=E∠∠BC=EF,AC=DF,C=F∠∠∴ΔABCΔDEF≌(第1题)练习:根据下列条件判断,下列三角形是否全等?(1)AC=DF,∠C=∠F,BC=EF(2)BC=BD,∠ABC=∠ABDAC=DC∠ACB=DCE∠BC=EC△ACBDCE(SAS)△AB=DEECBAD先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离。假设图中是一座大山,现在要穿过大山挖一条隧道AB,为了进行工程成本预算,需要量出AB的长度,你能利用所学知识量出AB的长度吗?BCDEA如图,已知AB=AC,AD=AE。求证:△ABD和△ACE证明:在△ABD和△ACE中(已知)=(公共角)=(已知)=AEADAAACAB∴△ABDACE≌△(SAS)∴∠B=∠C(全等三角形对应角相等)如图,AE=CF,∠AFD=∠CEB,DF=BE。求证:△AFD和△CEBFEDCBA证明:∵AE=FC∴AE-EF=FC-EF∴AF=EC∴△AFD≌△CEB(SAS)在△AFD和△CEB中ECAFCEBAFDBEDFBCDEA如图,已知AB=AC,AC=AE,∠BAE=DAC∠求证:△ABC和△ADE证明:∵∠BAE=DAC∠∴∠BAE+CAE=DAC+CAE∠∠∠∴∠DAE=BAC∠∴△ABC≌△ADE(SAS)在△ABC和△ADE中AEACBACDAEACAB1、在ΔABC中,AB=AC,AD平分∠BAC,试证明ΔABD全等于ΔACD。ABDC2、如图,已知ABED∥,AB=DE,AF=DC。求证:BC=EF。ABDCEF思考题:(选作)