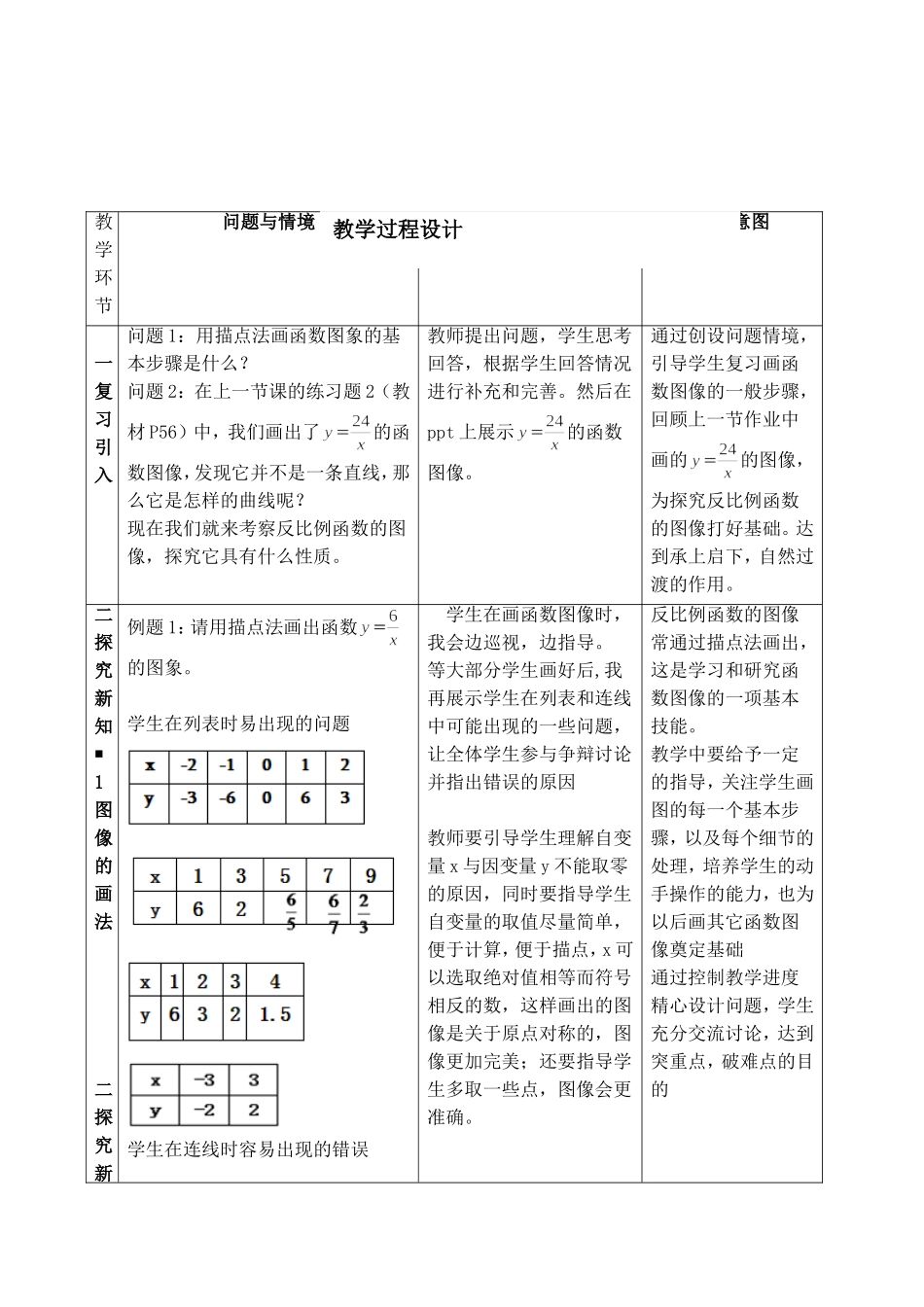
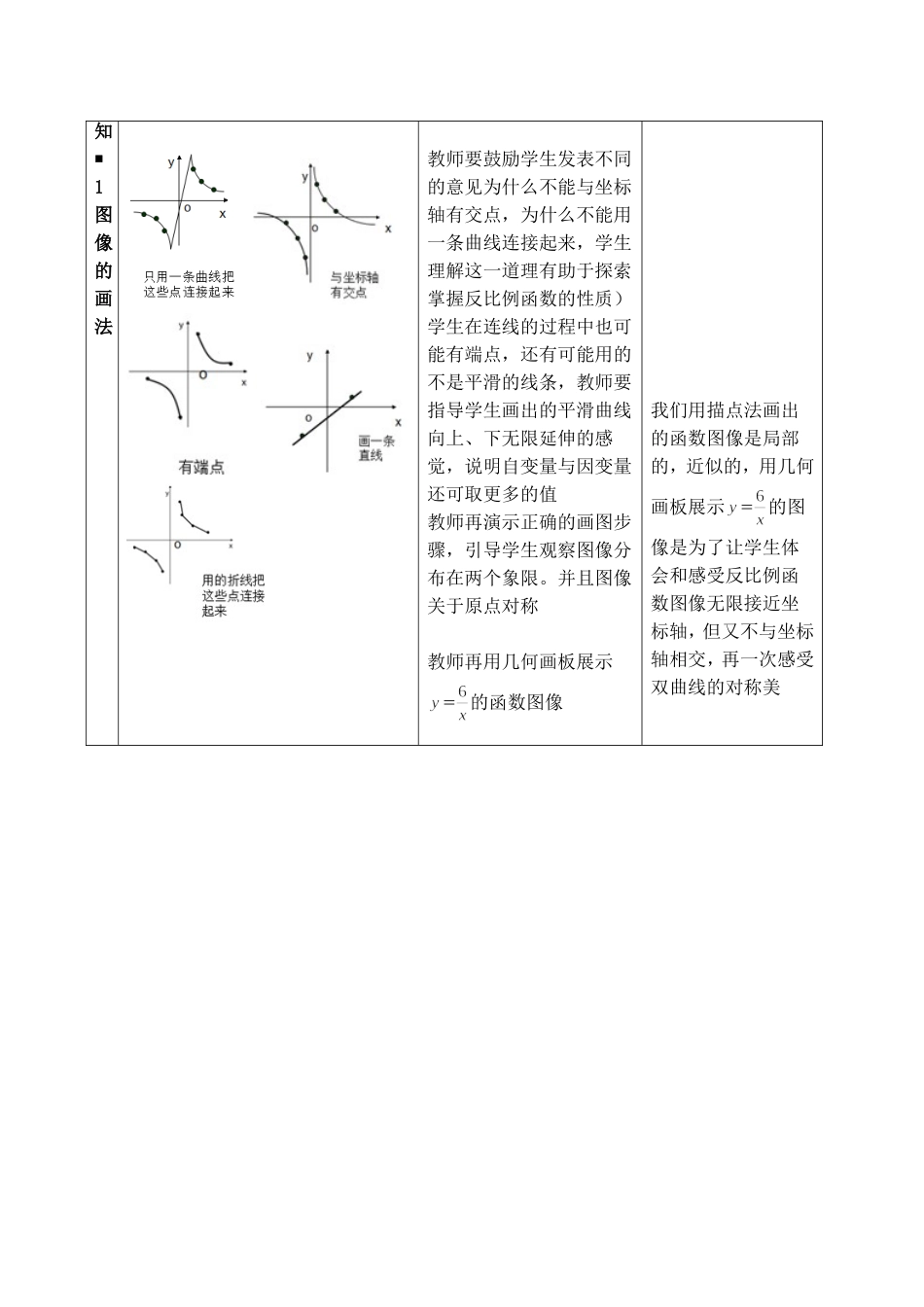
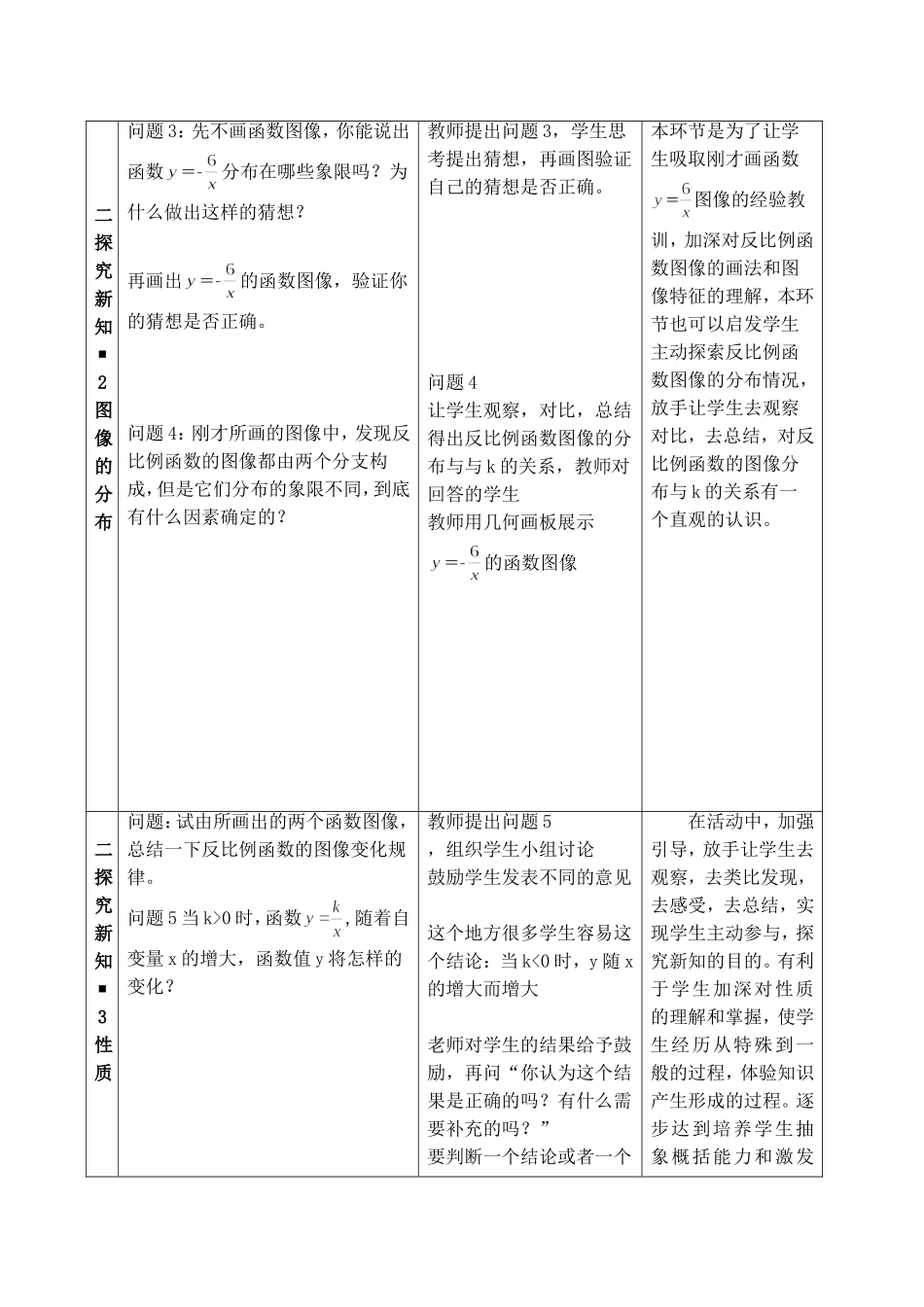
教学环节问题与情境师生活动设计意图一复习引入问题1:用描点法画函数图象的基本步骤是什么?问题2:在上一节课的练习题2(教材P56)中,我们画出了的函数图像,发现它并不是一条直线,那么它是怎样的曲线呢?现在我们就来考察反比例函数的图像,探究它具有什么性质。教师提出问题,学生思考回答,根据学生回答情况进行补充和完善。然后在ppt上展示的函数图像。通过创设问题情境,引导学生复习画函数图像的一般步骤,回顾上一节作业中画的的图像,为探究反比例函数的图像打好基础。达到承上启下,自然过渡的作用。二探究新知■1图像的画法二探究新例题1:请用描点法画出函数的图象。学生在列表时易出现的问题学生在连线时容易出现的错误学生在画函数图像时,我会边巡视,边指导。等大部分学生画好后,我再展示学生在列表和连线中可能出现的一些问题,让全体学生参与争辩讨论并指出错误的原因教师要引导学生理解自变量x与因变量y不能取零的原因,同时要指导学生自变量的取值尽量简单,便于计算,便于描点,x可以选取绝对值相等而符号相反的数,这样画出的图像是关于原点对称的,图像更加完美;还要指导学生多取一些点,图像会更准确。反比例函数的图像常通过描点法画出,这是学习和研究函数图像的一项基本技能。教学中要给予一定的指导,关注学生画图的每一个基本步骤,以及每个细节的处理,培养学生的动手操作的能力,也为以后画其它函数图像奠定基础通过控制教学进度精心设计问题,学生充分交流讨论,达到突重点,破难点的目的教学过程设计知■1图像的画法教师要鼓励学生发表不同的意见为什么不能与坐标轴有交点,为什么不能用一条曲线连接起来,学生理解这一道理有助于探索掌握反比例函数的性质)学生在连线的过程中也可能有端点,还有可能用的不是平滑的线条,教师要指导学生画出的平滑曲线向上、下无限延伸的感觉,说明自变量与因变量还可取更多的值教师再演示正确的画图步骤,引导学生观察图像分布在两个象限。并且图像关于原点对称教师再用几何画板展示的函数图像我们用描点法画出的函数图像是局部的,近似的,用几何画板展示的图像是为了让学生体会和感受反比例函数图像无限接近坐标轴,但又不与坐标轴相交,再一次感受双曲线的对称美二探究新知■2图像的分布问题3:先不画函数图像,你能说出函数分布在哪些象限吗?为什么做出这样的猜想?再画出的函数图像,验证你的猜想是否正确。问题4:刚才所画的图像中,发现反比例函数的图像都由两个分支构成,但是它们分布的象限不同,到底有什么因素确定的?教师提出问题3,学生思考提出猜想,再画图验证自己的猜想是否正确。问题4让学生观察,对比,总结得出反比例函数图像的分布与与k的关系,教师对回答的学生教师用几何画板展示的函数图像本环节是为了让学生吸取刚才画函数图像的经验教训,加深对反比例函数图像的画法和图像特征的理解,本环节也可以启发学生主动探索反比例函数图像的分布情况,放手让学生去观察对比,去总结,对反比例函数的图像分布与k的关系有一个直观的认识。二探究新知■3性质问题:试由所画出的两个函数图像,总结一下反比例函数的图像变化规律。问题5当k>0时,函数,随着自变量x的增大,函数值y将怎样的变化?教师提出问题5,组织学生小组讨论鼓励学生发表不同的意见这个地方很多学生容易这个结论:当k<0时,y随x的增大而增大老师对学生的结果给予鼓励,再问“你认为这个结果是正确的吗?有什么需要补充的吗?”要判断一个结论或者一个在活动中,加强引导,放手让学生去观察,去类比发现,去感受,去总结,实现学生主动参与,探究新知的目的。有利于学生加深对性质的理解和掌握,使学生经历从特殊到一般的过程,体验知识产生形成的过程。逐步达到培养学生抽象概括能力和激发二探究新知■3性质问题6:当k<0时,函数,随着自变量x的增大,函数值y将怎样的变化?命题是错误的,我们常常只需要举出一个反例就行了,所以这里可以教师引导学生举一个反例来说明刚才的得出的结论是不正确的,比如,反比例函数,当x=-2时,y=-3,当x=1,时,y=6,显然这与当k>0时,y随x的增大而减小矛盾;引导学生在每一个象限内去讨论...