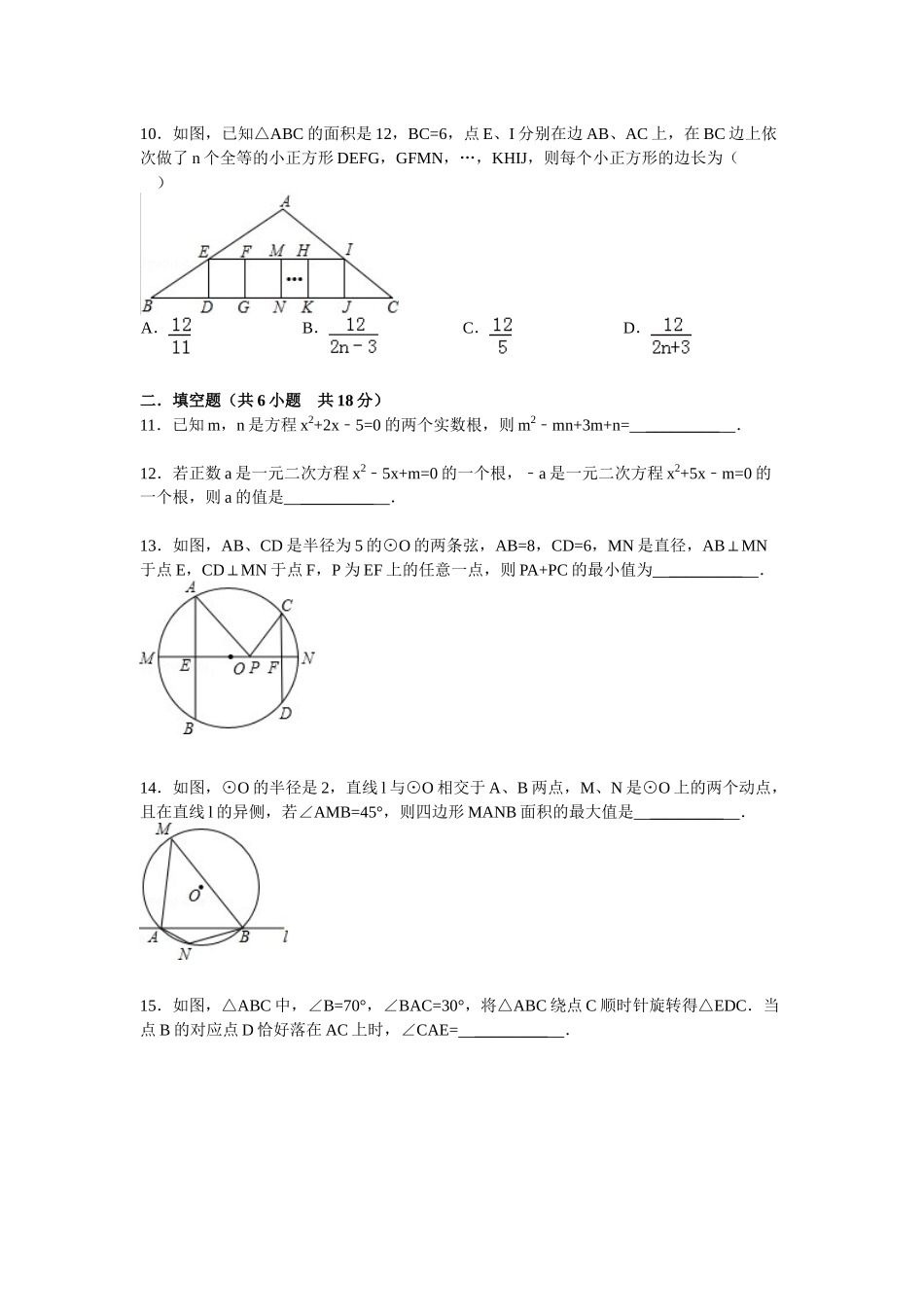
九年级上册数学试题一.选择题(共10小题共30分)1.下列银行标志中,既不是中心对称图形也不是轴对称图形的是()A.B.C.D.2.已知关于x的一元二次方程x2+ax+b=0有一个非零根﹣b,则ab﹣的值为()A.1B.1﹣C.0D.2﹣3.若关于x的一元二次方程(k1﹣)x2+2x2=0﹣有不相等实数根,则k的取值范围是()A.k>B.k≥C.k>且k≠1D.k≥且k≠14.已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图,其中正确的是()A.B.C.D.5.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:X1﹣013y1﹣353下列结论:(1)ac<0;(2)当x>1时,y的值随x值的增大而减小.(3)3是方程ax2+(b1﹣)x+c=0的一个根;(4)当﹣1<x<3时,ax2+(b1﹣)x+c>0.其中正确的个数为()A.4个B.3个C.2个D.1个6.如图,半径为3的⊙O内有一点A,OA=,点P在⊙O上,当∠OPA最大时,PA的长等于()A.B.C.3D.27.如图,⊙O的半径为1,△ABC是⊙O的内接等边三角形,点D、E在圆上,四边形BCDE为矩形,这个矩形的面积是()A.2B.C.D.8.如图,在直角梯形ABCD中,DCAB∥,∠DAB=90°,ACBC⊥,AC=BC,∠ABC的平分线分别交AD、AC于点E,F,则的值是()A.B.C.D.9.如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C的坐标为()A.(3,3)B.(4,3)C.(3,1)D.(4,1)10.如图,已知△ABC的面积是12,BC=6,点E、I分别在边AB、AC上,在BC边上依次做了n个全等的小正方形DEFG,GFMN,…,KHIJ,则每个小正方形的边长为()A.B.C.D.二.填空题(共6小题共18分)11.已知m,n是方程x2+2x5=0﹣的两个实数根,则m2mn+3m+n=﹣_________.12.若正数a是一元二次方程x25x+m=0﹣的一个根,﹣a是一元二次方程x2+5xm=0﹣的一个根,则a的值是_________.13.如图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,ABMN⊥于点E,CDMN⊥于点F,P为EF上的任意一点,则PA+PC的最小值为_________.14.如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是_________.15.如图,△ABC中,∠B=70°,∠BAC=30°,将△ABC绕点C顺时针旋转得△EDC.当点B的对应点D恰好落在AC上时,∠CAE=_________.16.如图,等腰RtABC△中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1,此时AP1=;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=2+;…,按此规律继续旋转,直至得到点P2014为止.则AP2014=_________.三.解答题(共9小题共72分)17.(6分)已知关于x的一元二次方程x22﹣x+m=0有两个不相等的实数根.(1)求实数m的最大整数值;(2)在(1)的条下,方程的实数根是x1,x2,求代数式x12+x22x﹣1x2的值.18.(6分)如图,AB是⊙O的直径,弦CDAB⊥于点E,点P在⊙O上,PB与CD交于点F,∠PBC=C∠.(1)求证:CBPD∥;(2)若∠PBC=22.5°,⊙O的半径R=2,求劣弧AC的长度.19.(8分)某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.(1)求转动一次转盘获得购物券的概率;(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算?20.(8分)如图的⊙O中,AB为直径,OCAB⊥,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.(1)求证:∠1=2∠.(2)已知:OF:OB=1:3,⊙O的半径为3,求AG的长.21.(6分)在13×13的网格图中,已知△ABC和点M(1,2).(1)以点M为位似中心,位似比为2,画出△ABC的位似图形△A′B′C′;(2)写出△A′B′C′...