相似三角形的判定SSS和SASVIP免费

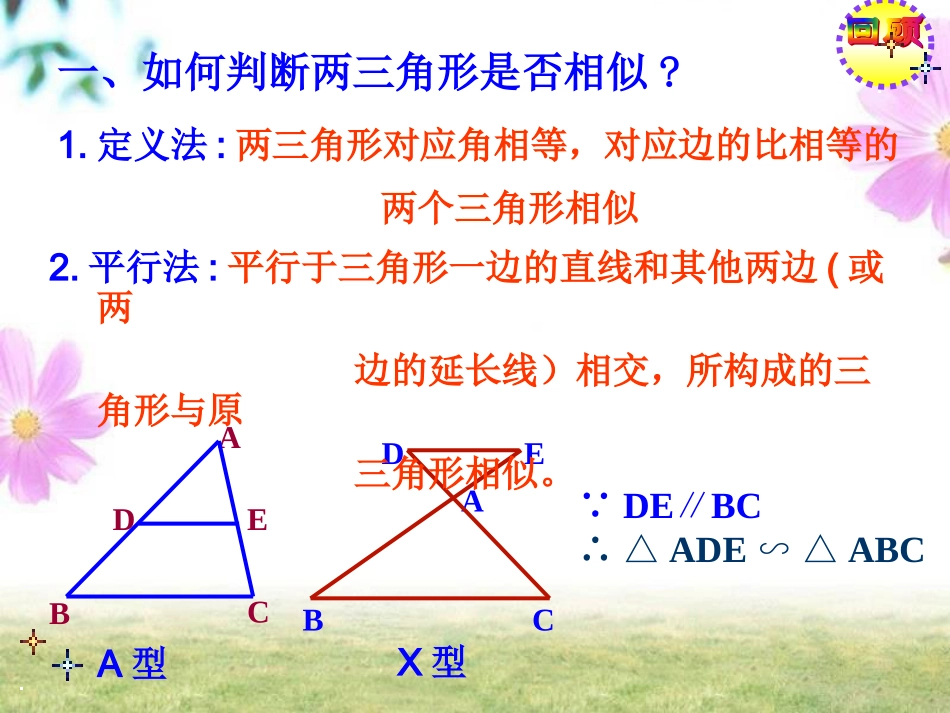
§27.2.1相似三角形的判定（SSS和SAS）1.定义法:两三角形对应角相等，对应边的比相等的两个三角形相似一、如何判断两三角形是否相似?∵DEBC∥∴△ADEABC∽△DEABCABCDE2.平行法:平行于三角形一边的直线和其他两边(或两边的延长线）相交，所构成的三角形与原三角形相似。A型X型猜想？有没有其他简单的办法判断两个三角形相似呢？二、三角形全等有哪几种简单的判定方法呢？SSS、SAS、ASA(AAS)、HLABCC’B’A’三组对应边的比相等ACC'A'BCC'B'ABB'A'是否有△∽△？'''CBAABC思考：能否借助平行线的判定方法？中，和已知：在'''CBAABC,''''''CAACCBBCBAABABC'''CBA求证:△∽△ABC'A'B'CDE''''''''CAEACBDEBADA∴又'''''CAACCAEAABDACAACCBBCBAAB',''''''∴同理BCDE∴∴，可得交于点交再做，过点上）截取（或它的延长线证明：在线段ECACBDEDABDABA'''''''∥DEA''''CBA∽ABCDEA'ABC∽'''CBA∴ACEA'∽'''CBAABC∽'''CBAABCkACC'A'BCC'B'ABB'A'（SSS）判定定理：如果两个三角形的三组对应边的比相等,那么这两个三角形相似.简单地说:三组对应边比相等的两三角形相似.ABC∽'''CBA'A'B'C例1：''''''CAACCBBCBAAB∴.12'',10'',6'',6,5,3'''CACBBAACBCABCBAABC否相似，并说明理由。是和根据下列条件，判断21126'',21105'',2163''CAACCBBCBAAB∵∴ABC∽'''CBA解：类似于用判定SSS的方法证明三角形相似，我们能不能判定两边及其夹角（SAS）证明两个三角形相似呢？猜想？的吗？这两个三角形还是相似若：.14'',10'',6'',6,5,3CACBBAACBCAB中，和已知：在'''CBAABC',''''AACAACBAABABC'''CBA求证:△∽△ABC'A'B'CDE''''''CAEABADA∴又DEDABDABA再做，过点上）截取（或它的延长线证明：在线段''''''''CAACCAEAABDACAACBAAB',''''∴∴∴∥，可得交于点交ECACB''''DEA''''CBA∽ABCDEA'ABC∽'''CBA∴ACEA'∽'''CBAABC∽'''CBA'.AA又(SAS)判定定理：如果两个三角形的两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似。ABC',C'A'ABB'A'AAAC'B'C'AABC∽'''CBA解∵AB/A’B’=7/3AC/A’C’=14/6=7/3∴AB/A’B’=AC/A’C’又∠A＝∠A’＝60°∴△ABCA`B`C`∽△AB=7，AC=14，∠A＝60°A’B’＝3，A’C’＝6，∠A’＝60°AB=7，AC=14，∠A＝60°A’B’＝6，A’C’＝3，∠A’＝60°例2：根据下列条件，判断△ABC和△A’B’C’是否相似，并说明理由。变式变式例3.右图中的两个三角形相似吗？理由是什么？练习：教材34页练习题练习：.5'',4'',3'',10,8,6)1('''CACBBAACBCABCBAABC否相似，并说明理由。是和根据下列条件，判断1.40'.6'',4''40,10,20)2(ACABAAACAB2.图中两个三角形是否相似？63105CABEE2693414相似不相似相似不相似要制作两个形状相同的三角形框架，其中一个三角形框架的三边长分别为4，6，8。另一个三角形框架的一边长为2，它的别外两条边长应当是多少？你有几种答案？3.提示：三种选法，分别使另一个三角形的长为2的边与长为4，6，8的边对应。2:4=x:6=y:8x:4=2:6=y:8x:4=y:6=2:8相似三角形的判定方法有几种？小结：1、定义判定法3、边边边判定法（SSS）4、边角边判定法（SAS）2、平行判定法比较复杂，烦琐只能在特定的图形里面使用