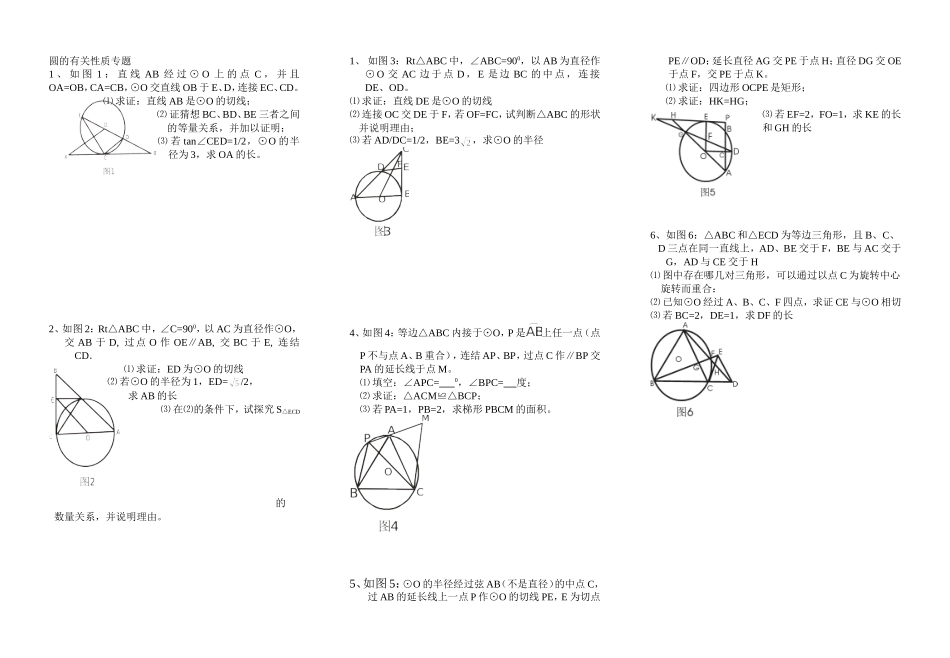
圆的有关性质专题1、如图1:直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E、D,连接EC、CD。⑴求证:直线AB是⊙O的切线;⑵证猜想BC、BD、BE三者之间的等量关系,并加以证明;⑶若tan∠CED=1/2,⊙O的半径为3,求OA的长。2、如图2:Rt△ABC中,∠C=900,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E,连结CD.⑴求证:ED为⊙O的切线⑵若⊙O的半径为1,ED=/2,求AB的长⑶在⑵的条件下,试探究S△ECD的数量关系,并说明理由。1、如图3:Rt△ABC中,∠ABC=900,以AB为直径作⊙O交AC边于点D,E是边BC的中点,连接DE、OD。⑴求证:直线DE是⊙O的切线⑵连接OC交DE于F,若OF=FC,试判断△ABC的形状并说明理由;⑶若AD/DC=1/2,BE=3,求⊙O的半径4、如图4:等边△ABC内接于⊙O,P是上任一点(点P不与点A、B重合),连结AP、BP,过点C作∥BP交PA的延长线于点M。⑴填空:∠APC=0,∠BPC=度;⑵求证:△ACM≌△BCP;⑶若PA=1,PB=2,求梯形PBCM的面积。5、如图5:⊙O的半径经过弦AB(不是直径)的中点C,过AB的延长线上一点P作⊙O的切线PE,E为切点PE∥OD;延长直径AG交PE于点H;直径DG交OE于点F,交PE于点K。⑴求证:四边形OCPE是矩形;⑵求证:HK=HG;⑶若EF=2,FO=1,求KE的长和GH的长6、如图6:△ABC和△ECD为等边三角形,且B、C、D三点在同一直线上,AD、BE交于F,BE与AC交于G,AD与CE交于H⑴图中存在哪几对三角形,可以通过以点C为旋转中心旋转而重合:⑵已知⊙O经过A、B、C、F四点,求证CE与⊙O相切⑶若BC=2,DE=1,求DF的长