根据图象求函数解析式VIP免费

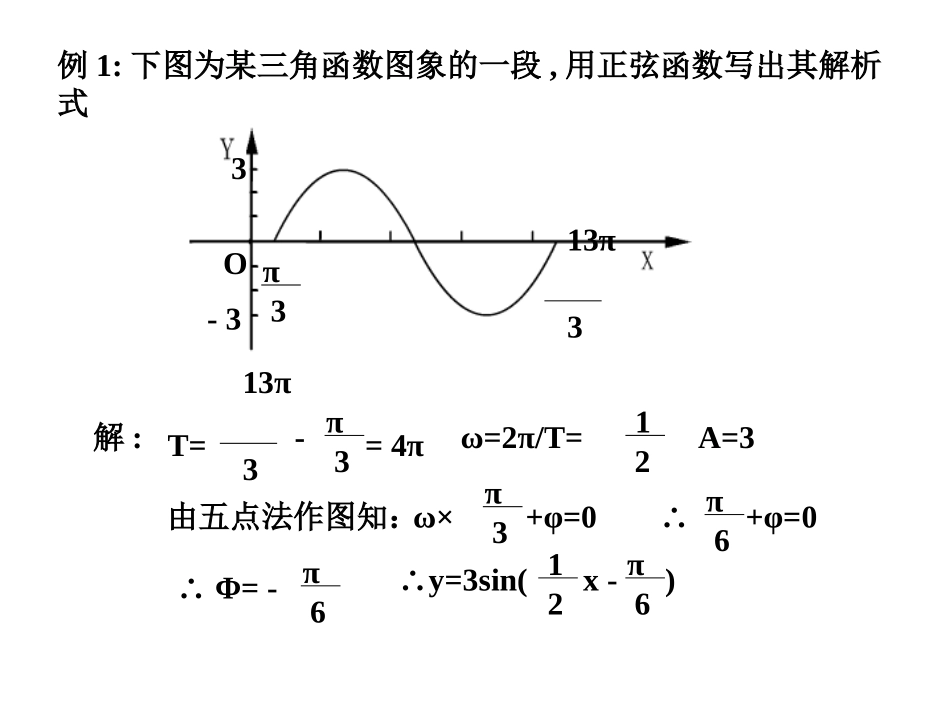
根据图象求函数解析式内容简析：由图象求解析式y=Asin(ωx+θ)+b时一般先确定平衡位置，再确定A，的大小，确定ω、θ时最好利用五点法中的某两个点。例1:下图为某三角函数图象的一段,用正弦函数写出其解析式-T==4π13π3π3ω=2π/T=12A=3∴+φ=0π6π6∴Φ=-∴y=3sin(x-)12π6ω×+φ=0π3由五点法作图知：解:13π3π3O3-3根据图象求函数解析式由函数y=Asin(ωx+θ)+b的图象求其解析式，一般来说，如对所求函数式中的A、ω、θ不加限制(如A、ω的正负，角的范围等)，那么所求的函数式应有无数多个不同的形式(这是由于所求函数是周期函数所致)，因此这类问题多以A>0,ω>0,|θ|<2形式出现，我们解这类题的方法往往因题而异，但逆用“五点法”作图的思想却渗透在各不同解法之中奎屯王新敞新疆函数解析式的确定关键在于参数A，ω，θ，b的确定。A：一般由图象的最高与最低点确定；ω与θ：一般由方程组ωx1+θ=0ωx2+θ=π2ωx3+θ=πωx4+θ=3π2ωx5+θ=2π中任意两个而确定（此法较简）；b由图象的平衡位置而定。解析：由图可知，点(0，1)和点(1211，0)都是图象上的点奎屯王新敞新疆将点(0，1)的坐标代入待定的函数式中，得2sin＝1，即sin＝21，又｜｜＜2，∴＝6又由“五点法”作图可知，点(1211，0)是“第五点”，所以ωx＋＝2π，即ω·1211π＋6＝2π，解之得ω＝2，故选C奎屯王新敞新疆的图像和性质xAysin63653-3---yxO【例3】如图函数y=Asin(ωx+确定A、ω、个函数解析式.)的图象，的值，确定其一解：（待定参数法）由图象知振幅A=3.又T=五、关于6π56πTπ2)2sin(3xy.,32),122sin(33,312Zkkyx时，)32sin(3xy取－（－）=π，∴ω==2，五、关于的图像和性质xAysin2【例4】若函数y=Asin（ωx+）（ω>0,的图象的一个最高点为（2,最低点之间的图象与x轴交于点（6,0），求>0））,它到其相邻这个函数的一个解析式.五、关于的图像和性质xAysin解：由题意有A=2,4,0,,43,0)43sin(,0)68sin(2,0)6(),8sin(2)(,8,162,16)26(4kzkkfxxfT取，且故所求函数的解析式为)48sin(2yxπ127-21O1:已知函数y=Asin(ωx+φ）（A>0,ω>0,│φ│<）的图象如图所示，确定该函数解析式π2解：由图知：A=2∵过（0，1）点∴2sinφ=1sinφ=φ=∴12π6由五点法作图知：－+φ=-πω=2∴7π12函数的解析式为y=2sin(2x+)π6∴π127-21O1:已知函数y=Asin(ωx+φ）（A>0,ω>0,│φ│<）的图象如图所示，确定该函数解析式π2练习：（全国高考题）如图所示函数y=2sin(ωx+φ）（│φ│<)的图象那么（）π2π6φ=-π121112O1011Φ=π6π6C.ω=2φ=D.ω=2A.ω=π6φ=1011B.ω=-解：该图象是向左平移而得到∴φ>0由A,C知φ=π6令ωx+=0得x=－<0∴点(－,0)在y轴左侧π6π6ωπ6ω∴－(-)=解得ω=211π12π6ω2πω（全国高考题）如图所示函数y=2sin(ωx+φ）（│φ│〈）的图象那么（）Φ=π6D.ω=21011A.ω=π6φ=1011B.ω=π6φ=-2πC.ω=2φ=π6-π121112O练习：如图所示为函数的部分图象．求出函数的解析式)2(,)sin(bxAyyx123-13212111)62sin(2xyminmax)()(21xfxfA①minmax)()(21xfxfb③T2②④利用最低点或最高点在图像上，该点的坐标满足函数解析式可得1奎屯王新敞新疆已知函数y＝Asin(ωx＋φ)在一个周期内，当x＝12时，取得最大值2，当x＝127时取得最小值－2，那么())62sin(2D.)62sin(2.C)32sin(2B.)3sin(21A.xyxyxyxy2奎屯王新敞新疆如图，已知函数y＝Asin（ωx＋φ）的图象(的部分)，则函数的表达式为()A奎屯王新敞新疆y＝2sin（61110x）B奎屯王新敞新疆y＝2sin（61110x）C奎屯王新敞新疆y＝2sin（2x＋6）D奎屯王新敞新疆y＝2sin（2x－6)三、热身练习BC010203061014xy例如图，某地一天从6~14时的温度变化曲线近似满足函数(1)求这一天6~14时的最大温差；(2)写出这段曲线的函数解析式。sin()yAxb一般的，所求出的函数模型只能近似刻画这天某个时刻的温度变化情况，因此应当特别注意自变量的变化范围。